TB6钛合金β区变形的动态再结晶动力学

doi:10.11901/1005.3093.2019.329

TB6钛合金β区变形的动态再结晶动力学

欧阳德来¹, 鲁世强¹, 崔霞^,¹, 徐勇¹, 杜海明², 朱慧安¹

1. 南昌航空大学材料科学与工程学院南昌 330063

2. 江西师范大学南昌 330022

Kinetics of Dynamic Recrystallization of TB6 Ti-Alloy During Hot Compressive Deformation atTemperatures of β-phase Range

OUYANG Delai¹, LU Shiqiang¹, CUI Xia^,¹, XU Yong¹, DU Haiming², ZHU Huian¹

1. School of Materials Science and Engineering, Nanchang Hangkong University, Nanchang 330063, China

2. Jiangxi Normal University, Nanchang 330022, China

通讯作者: 崔霞，副教授，cuixia2000@163.com，研究方向为航空结构材料组织、性能与成形工艺

责任编辑: 黄青

收稿日期: 2019-07-04 修回日期: 2019-09-13 网络出版日期: 2019-12-06

基金资助:

国家自然科学基金. 51761029
国家自然科学基金. 51864035

Corresponding authors: CUI Xia, Tel: (0791)83863039, E-mail:cuixia2000@163.com

Received: 2019-07-04 Revised: 2019-09-13 Online: 2019-12-06

Fund supported:

National Natural Science Foundation of China. 51761029
National Natural Science Foundation of China. 51864035

作者简介 About authors

欧阳德来，男，1977年生，副教授

摘要

使用圆柱形TB6钛合金试样在Thermecmaster-Z型热模拟试验机上进行热模拟压缩实验(变形温度为825~1100℃，应变速率为0.001~1 s^-1)。对采集的流变数据进行加工硬化率处理，确定动态再结晶体积分数，研究了TB6钛合金β区变形的动态再结晶动力学。结果表明，流变应力随着变形温度的降低或应变速率的提高而增大，流变曲线呈现出动态再结晶类型的特征。随着应变速率的降低和变形温度的提高，动态再结晶的体积分数和晶粒尺寸增大。在变形温度高于950℃、应变速率低于0.001 s^-1条件下，动态再结晶的晶粒严重粗化。动态再结晶动力学曲线经历缓慢增加—快速增加—缓慢增加三个阶段，呈现出典型的“S”型特征。确定了动态再结晶的体积分数达到50%时的应变，建立了TB6钛合金的动态再结晶动力学模型。

关键词： 金属材料 ; TB6钛合金 ; 加工硬化率 ; 动态再结晶 ; 动力学

Abstract

Hot compression tests of as-forged Ti-alloy TB6 were conducted via thermecmaster-Z hot simulation test machine through rapid heating the alloy up to the temperature range for the presence of β-phase and then compression tests by strain rates of 0.001~1 s^-1 at temperatures in the range of 825~1100℃, while the dynamic recrystallization (DRX) volume fraction were acquired by processing the collected rheological data during compression deformation with work hardening rate approach, then the kinetics of DRX of the alloy deformed at β-phase temperature was studied. The results show that the stress increases with the decrease of deformation temperature or the increase of strain rate, and the stress-strain curves present the type of DRX. With the decrease of strain rate and the increase of deformation temperature, the DRX volume fraction and the grain size of dynamic recrystallization increase. The DRX grain coarsening is observed for the alloy deformed at temperatures above 950℃ and strain rates below 0.001 s^-1. The DRX kinetics curves possess three typical stages: slow increase-fast increase-slow increase, showing a typical "S" type characteristic. Furthermore, the strain corresponding to the presence of 50% DRX volume fraction was determined and the relevant DRX kinetics model of TB6 Ti-alloy is established.

Keywords： metallic materials ; TB6 titanium alloy ; work hardening rate ; DRX ; Kinetics

PDF (6086KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

欧阳德来, 鲁世强, 崔霞, 徐勇, 杜海明, 朱慧安. TB6钛合金β区变形的动态再结晶动力学. 材料研究学报[J], 2019, 33(12): 918-926 DOI:10.11901/1005.3093.2019.329

OUYANG Delai, LU Shiqiang, CUI Xia, XU Yong, DU Haiming, ZHU Huian. Kinetics of Dynamic Recrystallization of TB6 Ti-Alloy During Hot Compressive Deformation atTemperatures of β-phase Range. Chinese Journal of Materials Research[J], 2019, 33(12): 918-926 DOI:10.11901/1005.3093.2019.329

动态再结晶(DRX)，是材料热变形过程中一种重要的冶金现象^[1,2]。消除合金内部的加工硬化对零件的成形性能有重要的影响，也是细化材料组织的主要手段^[3,4]。描述材料动态再结晶行为的主要参数，有动态再结晶临界应变、动态再结晶动力学和动态再结晶晶粒尺寸^[5]。动态再结晶动力学，是描述动态再结晶行为的重要参量之一^[6]。

TB6钛合金是一种近β亚稳型钛合金，名义成分为Ti-10V-2Al-3Fe^[7,8]。TB6钛合金具有比强度高、断裂韧性好、锻造温度低、淬透性好和抗应力腐蚀能力强等性能，适合制造飞机结构中的高强度锻件，如横梁、接头、滑轨、隔框和起落架等零部件^[9,10]。TB6钛合金发生在β相区温度热变形过程中的动态再结晶，可明显细化其变形组织并对其成形性能有重要的影响^[11,12]。在实际生产中，为了预测和控制该合金的动态再结晶发展过程，需要对其变形过程中的动态再结晶动力学进行定量化和模型化，因此必须测定热变形过程中的动态再结晶体积分数。通过观察热变形后高温“冻结”组织的金相组织^[13,14]和应力-应变数据的加工硬化率，可确定动态再结晶体积分数^[15]。但是，TB6钛合金的β相长大倾向大，低应变速率(如0.001 s^-1)时变形时间较长，发生动态再结晶的晶粒 “合并”和长大^[16]。在这种情况下，难以用金相法区别动态再结晶晶粒和原始晶粒，也就难以测量组织中实际动态再结晶体积分数。材料的应力应变数据是材料热变形时微观组织的外在表现，从应力-应变曲线得到的加工硬化率曲线才能反映材料内部组织变化特征^[17,18]，从而通过应力-应变数据的加工硬化率处理可确定材料动态再结晶体积分数^[19]。鉴于此，本文研究TB6钛合金β区变形的动态再结晶动力学，并建立动态再结晶动力学模型。

1 实验方法

实验用材料为经(α+β)两相区改锻的TB6钛合金棒材，用差热分析法测出(α+β)/β相变点为785±5℃。原始组织为β基体上分布着球状初生α相和细条状次生α相(图1箭头处)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 TB6钛合金原始棒材的组织

Fig.1 Microstructure of TB6 titanium alloy

在Thermecmaster-Z型热模拟试验机上将实验材料快速加热至β相区，保温210 s后进行等温恒应变速率热压缩实验，变形温度为825~1100℃，应变速率为0.001~1 s^-1。热模拟压缩设备自动记录和获取合金流动力学数据。

2 结果和分析

2.1 流变行为

图2给出了TB6钛合金在不同热变形条件下的应力-应变曲线。从图2可见，流变应力随着变形温度的降低或应变速率提高而增大。而流变应力的变化规律是，随着应变的增加流变应力快速增加后达到峰值。继续变形应力又下降而出现明显的应力峰，曲线呈现出单峰特征或动态再结晶型曲线特征。在本文的实验条件下曲线尾端还出现上翘现象，是变形后期压头与试样之间摩擦力增大所致。

图2

新窗口打开| 下载原图ZIP| 生成PPT

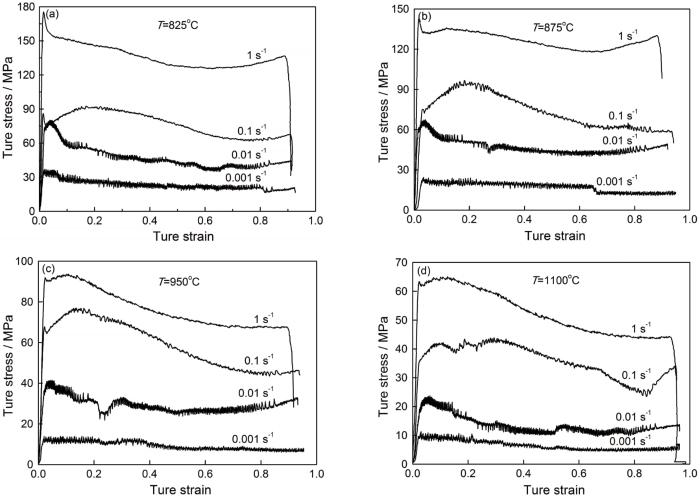
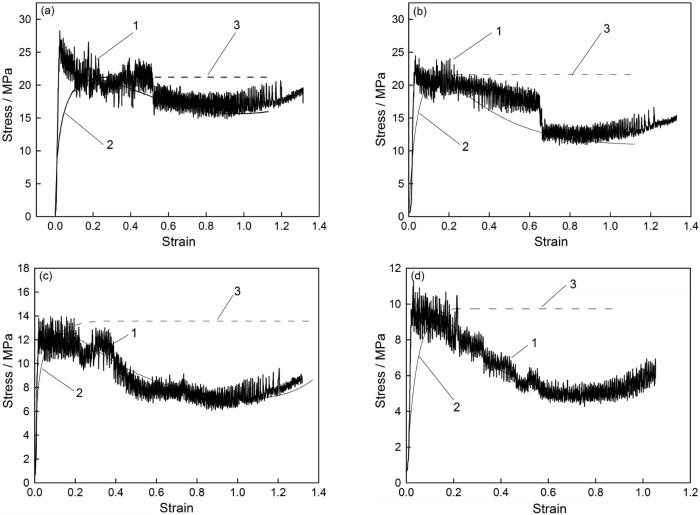
图2 TB6钛合金在不同热变形条件下的应力-应变曲线

Fig.2 True stress-true strain cures of TB6 alloy deformed at different deformation conditions

2.2 微观组织的演变

图3给出了TB6钛合金在不同热变形条件变形的金相组织。可以看出，合金在不同热变形条件下变形时发生了动态再结晶。热变形条件对合金动态再结晶组织有显著的影响。随着应变速率的增大动态再结晶体积分数降低，动态再结晶晶粒越细小。在变形温度为825℃、应变速率为0.001 s^-1条件下，合金的动态再结晶体积分数较高，约为81%，但是较低的应变速率使变形时间较长，动态再结晶晶粒及未发生动态再结晶β晶粒相互吞并、长大，此时变形组织并未明显细化，动态再结晶平均晶粒尺寸约为81.2 μm；应变速率增大到0.01 s^-1合金动态再结晶体积分数降低至约为65%，但是较短的变形时间使动态再结晶晶粒未明显长大。与应变速率为0.001 s^-1时相比变形组织反而更加细化，此时的动态再结晶平均晶粒尺寸约为40.6 μm；应变速率增大到0.1 s^-1合金动态再结晶体积分数降低至约为61%，与应变速率为0.01 s^-1时相比动态再结晶晶粒更细小，动态再结晶平均晶粒尺寸约为35.2 μm；应变速率提高到1 s^-1合金原始晶粒被拉长、压扁，只在原始晶界附近出现少量动态再结晶晶粒，晶粒也未细化。随着变形温度的提高动态再结晶体积分数增加，动态再结晶晶粒尺寸越大。在应变速率为0.001 s^-1、变形温度1100℃和950℃时，动态再结晶组织比825℃时明显粗化。值得注意的是，在较高的变形温度(>950℃)和较低应变速率(低于0.001 s^-1)条件下，动态再结晶晶粒长大或相互吞并，很难分辨变形组织中的动态再结晶晶粒，此时合金组织细化的效果仍然不明显。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 锻态TB6钛合金在不同热变形条件下的金相组织(ε=1.61)

Fig.3 Optical micrographs of specimens hot compressed with strain of 1.61: (a) 825℃,0.001 s^-1; (b) 825℃, 0.01 s^-1; (c) 825℃,0.1 s^-1; (d) 825℃, 1 s^-1; (e) 950℃, 0.001 s^-1; (f) 1100℃, 0.001 s^-1

2.3 根据加工硬化率确定DRX体积分数

采用加工硬化率方法确定DRX体积分数，是对应力-应变曲线用外推法估算动态再结晶体积分数^[20]为

X_{d R X} = \frac{(σ_{d r v x})^{2} - (σ_{d r x x})^{2}}{(σ_{d r v s s})^{2} - (σ_{d r x s s})^{2}}

(1)

其中 $σ_{d r v x}$ 、 $σ_{d r v s s}$ 分别为材料虚拟动态回复时某一时刻的应变ε_x和稳态应变ε_drvss对应的流动应力， $σ_{d r x x}$ 、 $σ_{d r x s s}$ 分别为材料发生动态再结晶时某一时刻的应变ε_x和稳态应变ε_drxss对应的流动应力，σ_c为材料发生动态再结晶时的动态再结晶临界应力，ε_c为材料发生动态再结晶时的动态再结晶临界应变(图4)。

图4

新窗口打开| 下载原图ZIP| 生成PPT

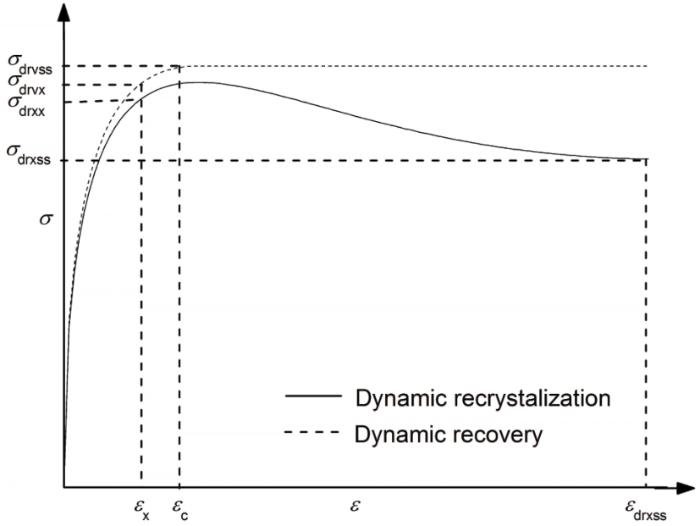
图4 动态再结晶和虚拟动态回复时的应力-应变曲线示意图

Fig.4 Schematic diagram of stress-strain curves for dynamic recrystallization and virtual dynamic recovery

将材料加工硬化率(θ=dσ/dε)曲线外推得到虚拟动态回复曲线，如图5所示。加工硬化率沿A-B-C变化，B为曲线拐点，也即材料发生动态再结晶临界条件点(θ_c为动态再结晶临界加工硬化率)。而当材料只发生动态回复时其加工硬化率沿A-B-D变化，其中BD为曲线ABC在B点的外推直线。此时，BD直线斜率与曲线ABC在B点的斜率相等。曲线ABD则为材料虚拟动态回复时的加工硬化率曲线。根据加工硬化率曲线ABD和θ=dσ/dε，可画出材料虚拟动态回复曲线。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 材料的加工硬化率曲线示意图

Fig.5 Schematic diagram of work hardening rate curve

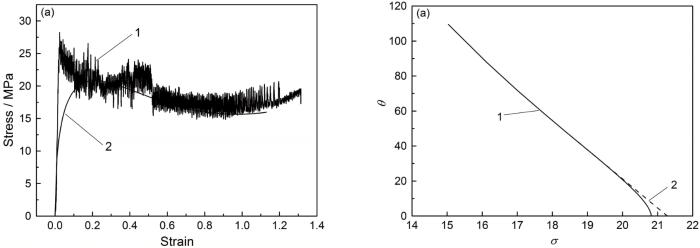
以变形温度为825℃、应变速率为0.001 s^-1时的应力-应变曲线为例，说明此方法。因为实际的应力-应变曲线不光滑(图6a)，难于直接对其加工硬化率(斜率)的测定，因此先对其应力-应变曲线进行拟合，拟合方程为

\begin{array}{l} σ = - 193.96 + 32.14 \times ε + 110.9 \times (ε^{0.5}) \\ + 193.97 \times e x p (- ε) \end{array}

(2)

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 TB6钛合金在变形温度为825℃、应变速率为0.001 s^-1条件下的应力-应变曲线和θ-σ曲线

Fig.6 Stress-strain curves (1-True curve, 2-Fitting curve) (a) and θ~σ curve (1-True curve, 2-Extrapolation curve) (b) of TB6 titanium alloy at deformation temperature 825℃ and strain rate 0.001 s^-1

为了对方程(2)简化处理，假设拟合曲线中两点间的应变差△ε很小，两点间的斜率近似地与该点的斜率相等。于是可使用方程(2)和dσ/dε≈△σ/△ε计算出对应于各应力(应变)下的加工硬化率。画出lnθ~ε曲线并将其外推，如图6b所示。根据外推加工硬化率曲线画出虚拟动态回复曲线，如图7a所示。根据材料虚拟动态回复曲线和实际应力-应变曲线和式(1)，可计算出不同应变下的动态再结晶体积分数，如图7b所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

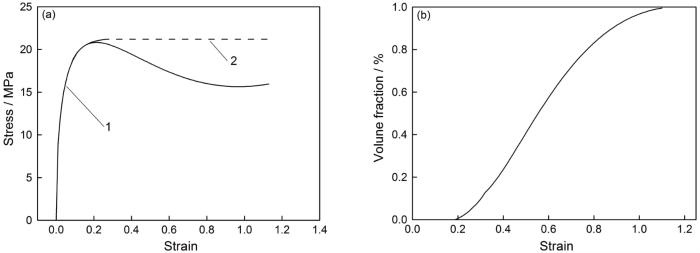
图7 TB6钛合金在应变速率为0.001 s^-1、变形温度为825℃条件下的应力-应变曲线和动态再结晶动力学曲线

Fig.7 Stress-strain curves (1- Fitting curve, 2-Virtual dynamic recovery curve) (a) and DRX kinetics curve (b) of TB6 titanium alloy at deformation temperature 825℃ and strain rate 0.001 s^-1

用动态再结晶体积分数确定方法并使用图2中的应力-应变数据，可画出TB6钛合金在应变速率0.001 s^-1时其它热变形温度下的应力-应变拟合曲线(图8)和θ-σ曲线(图9)，并计算出相应的动态再结晶体积分数。图10给出了用加工硬化率法画出的在应变速率为0.001 s^-1不同变形温度下的动态再结晶动力学曲线。可以看出，合金在应变速率为0.001 s^-1时，不同变形温度下的动态再结晶动力学曲线均呈现出“S”曲线特征，随着应变的增大动态再结晶体积分数先缓慢增加然后快速增大，最后又缓慢增大到100%。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 TB6钛合金在应变速率为0.001 s^-1不同变形温度条件下的应力-应变曲线

Fig.8 Stress-strain curves (1-True curve, 2-Fitting curve, 3-Virtual dynamic recovery curve)of TB6 titanium alloy at strain rate 0.001 s^-1 and different deformation temperatures (a) 825℃, (b) 875℃, (c) 950℃, (d) 1100℃

图9

新窗口打开| 下载原图ZIP| 生成PPT

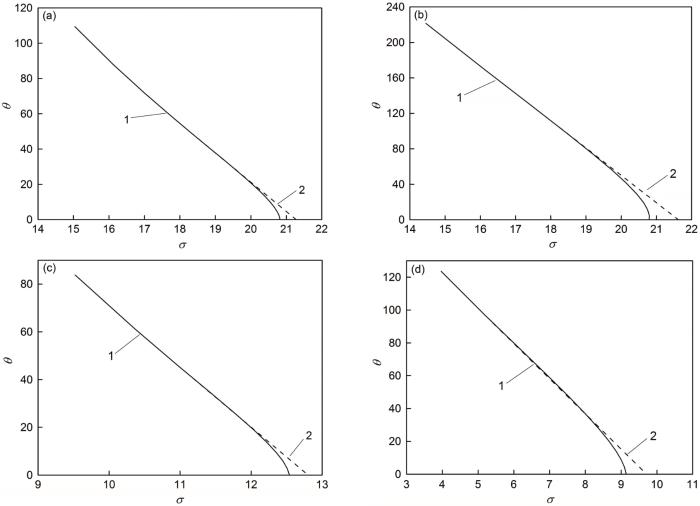
图9 TB6钛合金在应变速率为0.001 s^-1不同变形温度条件下的θ-σ曲线

Fig.9 θ-σ curves (1-True curve, 2-Extrapolation curve) of TB6 titanium alloy at strain rate 0.001 s^-1 and different deformation temperatures (a)825℃, (b) 875℃, (c) 950℃, (d) 1100℃

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 TB6钛合金在应变速率为0.001 s^-1不同变形温度条件下的动态再结晶动力学曲线

Fig.10 DRX kinetics curves of TB6 titanium alloy at strain rate 0.001 s^-1

2.4 DRX动力学模型

应变速率小于0.01 s^-1时合金动态再结晶晶粒长大不明显，动态再结晶晶粒可较清楚分辨。此时，采用直接微观组织观察法测量出对应的动态再结晶体积分数，并与用加工硬化率法确定的动态再结晶体积分数一起画出TB6钛合金不同热变形条件下动态再结晶动力学曲线，如图11所示。从图11可见，在不同变形温度和应变速率条件下，随着变形时间的增加合金动态再结晶体积分数经历缓慢增加—快速增加—缓慢增加三个典型阶段，动态再结晶动力学曲线呈现“S”型特征。因此，可用Avrami方程描述合金动态再结晶的动力学。

图11

新窗口打开| 下载原图ZIP| 生成PPT

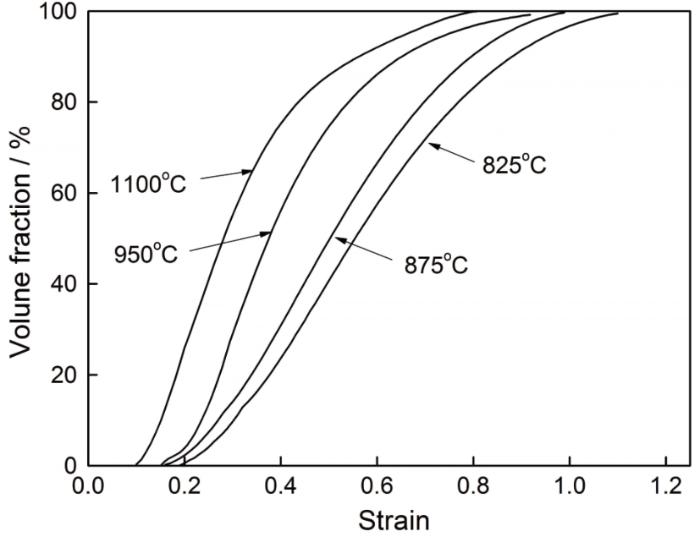
图11 TB6钛合金在不同热变形条件下的动态再结晶动力学曲线

Fig.11 DRX kinetics curves of TB6 titanium alloy at different deformation conditions

可采用Johnson-Mehl-Avrami(JMA)表达式

X_{d R X} = 1 - e x p [- k \times {(\frac{ε - ε_{c}}{ε_{0.5}})}^{n_{d}}], ε \geq ε_{c}

(3)

描述动态再结晶动力学模型。式中 $k$ 和n_d为材料参数；ε_c为动态再结晶临界应变， $ε_{0.5}$ 为动态再结晶达到50％时的应变。其中ε_c为^[12]

ε_{c} = 0.026735 \times [\dot{ε} \times e x p {(\frac{158000}{R T})]}^{0.0817}

(4)

式中a₁、a₂为与材料和变形参数有关的常数，R=8.314 J/mol·K为气体常数， $ε_{0.5}$ 为

ε_{0.5} = A_{1} {\dot{ε}}^{A_{2}} e x p (\frac{Q_{1}}{R T})

(5)

式中A₁、A₂为与材料和变形参数有关的常数，Q₁为变形激活能(J/mol)，R为气体常数。可使用合金动态再结晶动力学方程曲线估算ε_0.5值。以合金在变形温度为825℃、应变速率为0.01 s^-1时的动态再结晶动力学曲线为例(图12)，说明ε_0.5值的确定。对图12中的动态再结晶体积分数实测数据进行Avrami模型 $X_{d R X} = 1 - e x p (- B \times t^{n})$ 结构拟合，其中B、n为常数，t为变形时间。此时，动态再结晶动力学拟合方程为 $X_{d R X} = 1 - e x p (- 0.00003819 \times t^{2.04})$ 。取 $X_{d R X} = 0.5$ 则 $t \approx 120 s$ ，于是得 $ε_{0.5} \approx 120 \times 0.01 + ε_{c} = 1.2 + 0.063 = 1.263$ 。采用相同的方法和图11所示的不同热变形条件下动态再结晶动力学曲线，可确定其它热变形条件下的ε_0.5，如图13所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

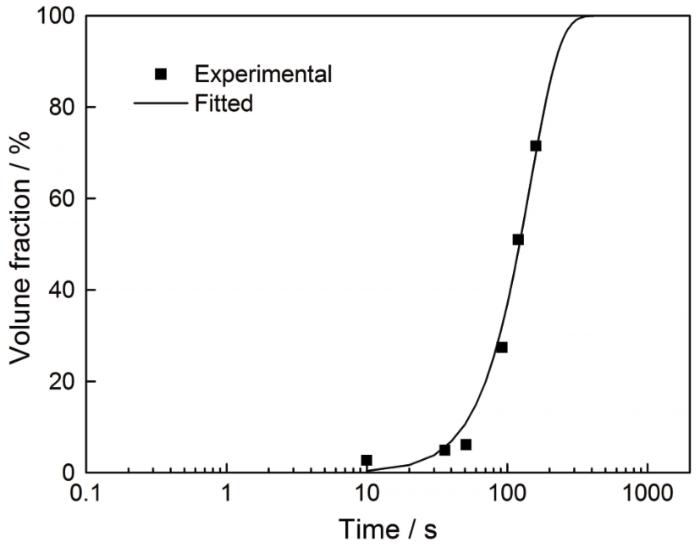
图12 TB6钛合金在825℃、应变速率为0.01 s^-1条件下的动态再结晶动力学曲线

Fig.12 DRX kinetics curve of TB6 titanium alloy at deformation temperature 825℃ and strain rate 0.01 s^-1

图13

新窗口打开| 下载原图ZIP| 生成PPT

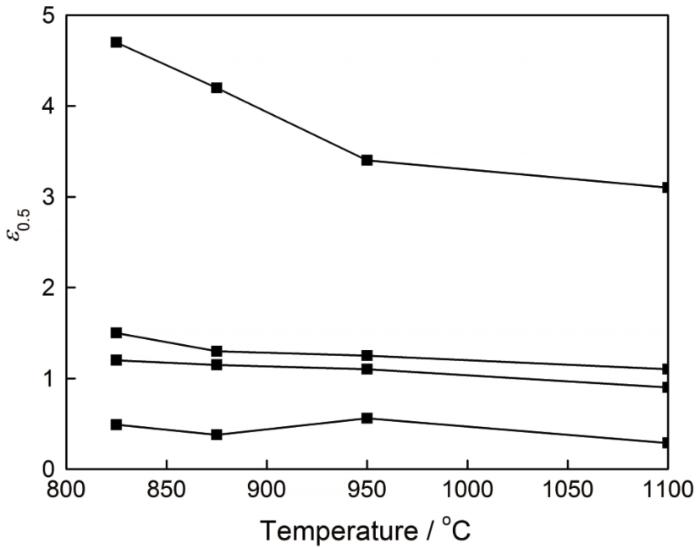
图13 TB6钛合金在不同热变形条件下的动态再结晶ε_0.5值

Fig.13 ε_0.5value of TB6 titanium alloy at different deformation conditions

确定不同热变形条件下的ε_0.5值后按式(5)进行拟和，得到式(5)中的参数A₁＝0.54326，A₂＝0.35775，Q₁＝19230.8 J/mol。于是ε_0.5可表示为

ε_{0.5} = 0.54326 {\dot{ε}}^{0.35775} e x p (\frac{19230.8}{R T})

(6)

对式(3)两边取自然对数 $l n [- l n (1 - X_{d R X})] = l n (k) + n_{d} \times l n (\frac{ε - ε_{c}}{ε_{0.5}})]$ ，根据图5中不同热变形条件下的动态再结晶体积分数数据和式(4)、式(6)的ε_c、ε_0.5数据，画出合金的ln[-ln(1-X_dRX)]与ln[(ε-ε_c)/ε_0.5]的关系曲线。由此可确定式(3)中的 $l n k$ =0.54和n_d=0.9，也即k=0.58。于是TB6钛合金动态再结晶体积分数模型可表示为

X_{d R X} = 1 - e x p [0.58 \times {(\frac{ε - ε_{c}}{ε_{0.5}})}^{0.9}], ε \geq ε_{c}

(7)

其中

ε_{c} = 0.232 {\dot{ε}}^{0.048} e x p (\frac{18241}{R T})

，

ε_{0.5} = 0.54326 {\dot{ε}}^{0.35775} e x p (\frac{19230.8}{R T})

。

图14

新窗口打开| 下载原图ZIP| 生成PPT

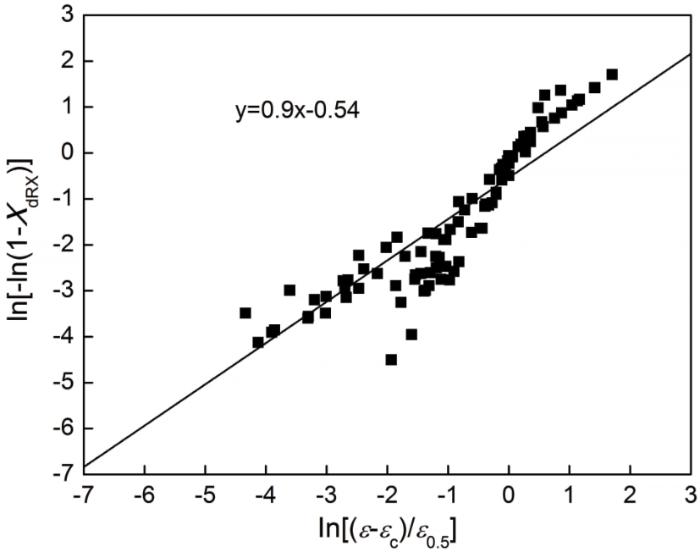
图14 ln[-ln(1-X_dRX)]与ln[(ε-ε_c)/ε_0.5]的关系曲线

Fig.14 Relation of ln[-ln(1-X_dRX)] and ln[(ε-ε_c)/ε_0.5]

3 结论

(1) TB6钛合金的流变应力随着变形温度的降低或应变速率的提高而增大，流变曲线呈现出动态再结晶类型特征。

(2) 随着应变速率的降低和变形温度的提高TB6钛合金的动态再结晶体积分数增加，动态再结晶晶粒尺寸大。在变形温度高于950℃、应变速率小于0.001 s^-1的条件下，动态再结晶晶粒明显粗化。

(3) 根据对TB6钛合金的应力应变数据进行加工硬化率处理画出的虚拟动态回复曲线，可确定合金动态再结晶体积分数。

(4) TB6钛合金的动态再结晶动力学曲线经历缓慢增加—快速增加—缓慢增加三个典型阶段，呈现出典型的“S”型特征。

(5) 本文建立的TB6钛合金动态再结晶动力学模型为 $X_{d R X} = 1 - e x p [0.58 \times {(\frac{ε - ε_{c}}{ε_{0.5}})}^{0.9}]$ ，其中， $ε_{c} = 0.232 {\dot{ε}}^{0.048} e x p (\frac{18241}{R T})$ ， $ε_{0.5} = 0.54326 {\dot{ε}}^{0.35775} e x p (\frac{19230.8}{R T})$ 。