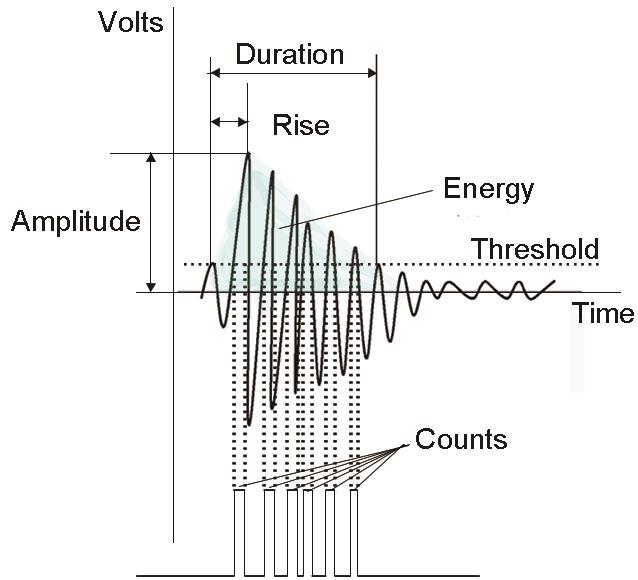
声发射仪器能记录、存储和分析声发射波并将其转换为数字信号[11,14,15],即声发射信号。声发射信号,由上升时间、持续时间、计数、幅度、能量、绝对能量等参数组成[9,11,24]。典型声发射参数的定义,如图1所示。图1中的震荡曲线是检测到的突发型声发射波,其高于背景噪声的门槛电压,称为阈值(Threshold),信号每次超过阈值称为一次撞击(Hit)。将信号第一次超过阈值到最大振幅经历的时间间隔称为上升时间(Rise time),常用于鉴别噪声;将信号第一次超过阈值到最后一次降至阈值经历的时间间隔称为持续时间(Duration),也用于噪声鉴别;将信号幅度超过阈值的次数称为振铃计数(Counts)[24],粗略反映信号的强度和频度,用于评价声发射活动;将信号波形的最大振幅值称为幅度(Amplitude),用于波源的类型鉴别、强度及衰减的测量;能量(Energy)通常指的是能量计数,是信号幅值包络线下的面积,反应事件的相对能量或强度;而绝对能量(Absolute energy)是信号幅值平方围成的包络线面积,能真实反应声发射源以弹性波形式释放的能量[25]。
图1
早期准确识别即将到来的临界损伤阶段,对于避免过早失效至关重要[9,13,15,26]。目前已有大量的工作根据声发射参数特征定性评估疲劳裂纹扩展过程中的损伤[14,24,27~42]。声发射参数中的计数是评估疲劳损伤的首选参数[14,24,27~31],如振铃计数[2,14,16,43,44]、能量计数[2,14,43]和事件计数[8]等。计数有处理简便、能粗略反映信号强度和频度等优点,可用于评价声发射活动性,但是受阈值和噪声的影响[16,25,43]。也有学者用计数、持续时间、上升时间、能量和幅值综合分析不锈钢的疲劳裂纹扩展特性[14]。声发射信号参数中的绝对能量,也可用于检测[32,33,41]和预测[5,45]疲劳裂纹扩展。Nemati等[33]认为,绝对能量对阈值设置的依赖性较小。Yu等[5]和Zárate等[41]认为,绝对能量率比计数率更适合于预测材料的疲劳寿命。有的学者提出新的声发射参数,如Aggelis等[34]用RA值(上升时间与振幅之比)评估金属板的疲劳损伤。Keshtgar等[40]提出声发射强度,是将计数、振幅和振幅阈值相结合用于评估小裂纹的扩展。但是,在疲劳试验或工程结构运行等监测过程中用于评估疲劳损伤的传统声发射参数,严重依赖阈值和参数设置并受波传播介质和衰减特性的影响[9,11,24],特别是计数和能量等参数的分散性很大[16]。参数设置不当对声发射结果有较大的影响,增大疲劳损伤和疲劳寿命评估的不确定性[9]。
旋转机械的转速固定,使部件金属发生疲劳的载荷属于周期载荷。实验结果表明,在金属疲劳断裂过程中产生的信号通常是非线性、随机性和耗散性的,用传统的线性理论分析方法不能很好地揭示金属疲劳损伤过程。因此,必须研究周期载荷状态下金属疲劳特性的声发射混沌特性。已有一些与声发射信号混沌特性的相关研究涉及机械运行状态[46~49]和部件磨损[50~52],作为故障识别和疲劳预测的方法。Mao等[53]认为:“熵表征物质系统状态的丰富程度,称为复杂程度”。而Kolmogorov熵(简称K熵)则表征系统信息的平均损失率,计算K熵可给出系统的分类[54,55]。Huang等[8]用K熵分析声发射信号,发现金属疲劳损伤过程中的声发射信号存在混沌现象,混沌特性变化与疲劳损伤过程有较强的关联性。也就是,声发射信号的K熵能较好的揭示金属疲劳损伤过程的动力学特性,可作为表征金属疲劳损伤程度的特征量。鉴于此,本文基于K熵的特质提出二次K熵方法,分析高温合金疲劳扩展过程这的声发射信号并做进一步处理,使其扩展特征更加明显和易于分析疲劳扩展特征。
1 K熵的计算
K熵是表征非线性系统变化的一种特征量,度量系统的混沌程度,能从数值K上区分系统的动力学类型。K = 0的系统呈规则运动,K > 0的系统呈混沌运动,K = ∞的系统呈随机运动。系统的K值越大表明其相应的信息损失率越大,混沌程度越高[51],即系统越复杂。用于K熵计算的方法有两个,一个是Grassberger和Procaccia 1983年提出的饱和关联维数法[56],另一个是Schouten 1994年提出的极大似然估计法[57]。本文采用极大似然估计法计算K熵。此法计算较简单、计算过程较快且无二异性,适于工程应用。极大似然估计法假设,一对不同轨道上的初始邻近点的间距从足够小分离至大于
式中K为K熵(以e为底时K熵的单位为nats/s;以2为底则K熵的单位为bits/s),b为初始邻近点的间距第一次超过
假设实际测得的声发射信号是长度为N的时间序列{x1, x2,···, xN},选取适当的嵌入维数
上述m维相空间中的一对相点
满足|xi - xj | < r0时计算出{|xi + 1 - xj + 1|, |xi + 2 - xj + 2|,···, |xi + m - 1 - xj + m - 1|}中小于r0的连续数据的个数,即为所求的b值。{|xi + t - 1 - xj + t - 1|}≤ r0且|xi + t - xj + t | > r0时,t即为所求的b。
经过
在遍历
用
嵌入维数
2 实验方法
低周疲劳拉-拉实验用试棒,是标准高温合金。根据国家标准GB/T 15248-2008的规定制作试样,其尺寸在图2中给出。
图2
疲劳实验在型号为300DX的静态液压万能试验机上进行,加载频率10 Hz,误差小于1%,最大载荷为300 kN,两个传感器分别放置于试验夹具上,如图3所示。
图3
图3
Instron-300DX静态液压万能试验机及试验设备的描述
Fig.3
Instron-300DX static hydraulic universal testing machine and test equipment description
采用美国物理声学公司(PAC)生产的第三代全数字化系统SAMOS(PCI-8)声发射检测系统(图4)监测疲劳裂纹扩展过程中的声发射信号。每通道有4个高通、4个低通模拟滤波器,16位A/D精度。门槛值为40 dB,前置放大增益为40 dB,带宽为100 kHz~400 kHz,采样率为1 MHz,峰值鉴别时间PDT为300 μs,撞击鉴别时间HDT为600 μs,撞击闭锁时间HLT为1000 μs。能采集到8种基本特征参数,其中6种包括上升时间、计数、能量、幅值、信号强度和绝对能量。
图4
3 实验结果
用高温合金试棒进行低周疲劳实验,用三个传感器分别测出该过程的三组声发射信号。从试件进行低周疲劳试验开始记录数据直到失稳断裂,历时3658.025 s。图5给出了断裂的高温合金试棒,可见断裂处的疲劳源。
图5
图6
图7
图8
(1) 声发射对初始值敏感。虽然疲劳初始裂纹成核、萌生阶段的声发射信号微弱且持续时间短,也能检测到,为尽早预测提供数据基础;
(2) 金属试棒的疲劳源极小,几乎是瞬断。只有在疲劳断裂前的数十到数百循环声发射信号的异常才较为明显,用传统方法很难做到早期疲劳预警;
(3) 断裂前各阶段声发射信号的趋势特征不明显、波动跨度范围大,无法有效实时判断疲劳损伤的发展程度,从而增加了分析和预测其趋势的困难。
因此,利用试验采集的声发射数据区分失稳断裂前的各阶段,分析其特点和趋势,尽早判断疲劳断裂的发生进而降低金属疲劳扩展断裂所带来的危害和损失,极为必要。
4 讨论
为了确定有表征金属疲劳过程优势的声发射参数,本文对上述各参数做变异系数计算,结果列于表1。在三个声发射信号采集通道的六个参数中,计算出的绝对能量的变异系数均最大。这表明,绝对能量包含的动态信息较多、不规则程度较高,与其他5个参数相比能更好地用描述混沌程度,从而使其包含的信息变化(即混沌程度)能更好地表征金属疲劳裂纹的扩展趋势。因此,将其用于分析本文的实验数据。
表1 不同通道声发射参数的变异系数
Table 1
| Channel | Rise time | Count | Energy | Amplitude | Signal strength | Absolute energy |
|---|---|---|---|---|---|---|
| Channel 1 | 2.2974 | 6.9948 | 2.2784 | 0.0237 | 2.6561 | 15.0792 |
| Channel 2 | 2.5457 | 21.2042 | 36.6878 | 0.0364 | 33.7580 | 460.7285 |
| Channel 3 | 2.3525 | 5.9017 | 2.5810 | 0.0271 | 2.6117 | 27.8711 |
通道1和通道3采集的声发射数据其数量多于通道2采集的一半,表征疲劳裂纹扩展过程以及进行计算时效果更好,因此本文采用这两个通道的数据。图9给出了这两个通道采集的声发射绝对能量参数的放大后的趋势图。为了便于观察绝对能量参数的原始细节特征,与处理后的结果对比。
图9
图9
通道1和通道3的声发射绝对能量的放大图
Fig.9
Magnification of acoustic emission parameter absolute energy in channel 1 (a) and channel 3 (b)
将两个通道的声发射数据分成相同数量的组,分别根据第2部分的计算方法计算出每组的K熵值,并将每组声发射数据中位数对应的时间作为所计算的K熵对应的时间。
(1) 一次K熵
分别对通道1和通道3的声发射绝对能量信号参数做第一次K熵计算,选取的临界阈值
图10
图10
通道1和通道3绝对能量的一次K熵计算结果
Fig.10
Calculation results of the first K-entropy of absolute energy parameters in channel 1 (a) and channel 3 (b)
图10给出了对声发射信号做第一次K熵计算的结果。可以看出,K熵的数值均大于0。据此可以判定,金属损伤过程中的声发射绝对能量具有混沌特性,且两通道K熵的趋势具有一致性,显著提高了疲劳过程变化的显著性。在约100 s前的一个很短的时间范围内,K熵的数值及其波动很小;在100~2500 s的一个较长的时间范围内K熵的数值将其波动均有所增大,但是始终保持在一个稳定上升的状态;在2500~3300 s的一个较短的时间范围内K熵的数值和波动变化进一步增大,比前一个阶段的变化较为剧烈;在约3300 s后K熵接近于0。定性分析结果表明,两通道的K熵在不同时间范围的变化趋势均与疲劳裂纹扩展的过程有一定的对应关系,即裂纹的萌生、缓慢扩展、快速扩展以及疲劳断裂这四个阶段。因此,声发射绝对能量参数的K熵变化趋势能表征疲劳裂纹的扩展过程。
同时,由图10可见,疲劳断裂的发生不再有突跃点,取而代之的是在疲劳断裂前出现K熵的最高点,为疲劳断裂的早期预测提供了可能。但是,对声发射信号仅做一次K熵,其计算的结果仍有较大的波动性和分散性,且不同的采样分组方案计算出的动力学表征结果有一定的差异。因此,在动态监测的过程中不易准确判断断裂前最高点的位置。与原始声发射信号对比表明,一次K熵随疲劳裂纹扩展的整体趋势变化更为明显,表现为数值和波动范围逐渐变大,其不规则程度也相应变大。由此可以判断,K熵数据也可能蕴含一定的动态信息和混沌特性。因此,本文尝试对一次K熵结果做第二次K熵计算,计算结果称为“二次K熵”。
(2) 二次K熵
本文提出的二次K熵方法,即对具有混沌特性的时序数据计算两次K熵以进一步得到更准确表征其动力学特征的方法。分别对通道1 和通道3声发射信号的第一次K熵计算结果做第二次K熵计算,数据量和数据值变化选取的参数也随之改变。临界阈值
图11
图11
通道1和通道3绝对能量的二次K熵计算结果
Fig.11
Calculation results of the quadratic K-entropy of the absolute energy parameters in channel 1 (a) and channel 3 (b)
图11表明,在约2500 s前二次K熵值在一个较长的时间范围内较为平稳地波动上升,在约2500~3300 s二次K熵值在一个较短的时间范围内较为剧烈的波动,在约3300 s后二次K熵值骤降至低点。这个结果,与前文的疲劳裂纹扩展过程仍然一致。由于疲劳裂纹的萌生是一个持续时间很短的过程,二次K熵受计算数量的限制。这里将约前2500 s与裂纹萌生和缓慢扩展过程对应,将2500~3300 s与裂纹快速扩过程对应,将大约3300 s后与裂纹失效断裂对应。因此,二次K熵仍然能表征疲劳裂纹的扩展过程。
图12
图12
通道1和通道3二次K熵的最高点与声发射参数突跃点位置的对比
Fig.12
Highest point of quadratic K-entropy vs. the jump point of acoustic emission signal in channel 1 (a) and channel 3 (b)
虽然二次K熵的计算结果损失了对裂纹萌生阶段的细节表征,但是得到了更加清晰明确的对疲劳裂纹扩展的整体表征,尤其是对疲劳断裂前最高点的确定更优于一次K熵的计算结果。这表明,对于疲劳断裂的预测,二次K熵方法有更加突出的优势。
关于原始声发射绝对能量参数的趋势,通道1和通道3临近破坏时的突跃点均出现在第3315.08 s,如图12所示。计算结果表明,二次K熵的两个最高点与原始声发射信号突跃点的时间分别提前了269.25 s和305.91 s,提前率分别为8.12%和9.23%。这表明,用二次K熵法能提前得到金属疲劳临近断裂前的信息,为预测金属疲劳裂纹的扩展和寿命提供依据。
5 结论
(1)绝对能量参数包含的动态信息最丰富,更适于研究金属疲劳损伤的声发射信号的混沌特性。
(2)对于不同的疲劳损伤程度,K熵的计算数值始终大于0,表明金属疲劳损伤的声发射信号具有混沌特性且一次K熵的时序趋势与金属疲劳损伤裂纹扩展过程具有对应关系,表明声发射信号的混沌特性能表征金属疲劳损伤过程。二次K熵虽然对裂纹扩展的萌生不敏感,但其时序趋势与金属疲劳裂纹扩展整体过程的对应关系比一次K熵更明显,尤其对疲劳断裂前的表征更精确。
(3)用本文提出的二次K熵方法对声发射信号做进一步处理,可得到疲劳断裂前的最高点,比疲劳断裂时的原始声发射信号的突跃点提前了8%以上。二次K熵方法不仅能动态检测金属疲劳过程,还能提供一种新的表征金属疲劳损伤程度的特征量,可为利用其演化规律预测金属疲劳扩展及寿命提供依据。
参考文献
Initiation and propagation characteristics of multi-source fatigue crack in superalloy disk
[J].
高温合金盘多源疲劳裂纹萌生及扩展特征
[J].
Acoustic emission technique for the detecting of metal fatigue fracture
[J].
金属疲劳断裂的声发射检测技术
[J].
Application of acoustic emission technology in study of fatigue fracture of metals
[J].
声发射技术在金属疲劳断裂研究中的应用
[J].
A new method for detecting fatigue crack initiation in aluminum alloy using acoustic emission waveform information entropy
[J].
Prediction of fatigue crack growth in steel bridge components using acoustic emission
[J].
Acoustic emission during fatigue of Ti-6Al-4V: incipient fatigue crack detection limits and generalized data analysis methodology
[J].
Detection of the onset of fatigue crack growth in rail steels using acoustic emission
[J].
Feature analysis for acoustic emission signals during metal fatigue damage based on Kolmogorov entropy and correlation dimension
[J].
基于K熵和关联维数的金属疲劳损伤过程的声发射信号特征分析
[J].
Assessment of fatigue crack growth in 316LN stainless steel based on acoustic emission entropy
[J].
Study of fatigue crack characteristics by acoustic emission
[J].
A new qualitative acoustic emission parameter based on Shannon's entropy for damage monitoring
[J].
Research and applications of AE on advanced composites
[J].
Advanced structural health monitoring of concrete structures with the aid of acoustic emission
[J].
Acoustic emission studies for characterization of fatigue crack growth in 316LN stainless steel and welds
[J].
Fatigue crack growth of Q345B using acoustic emission technique
[J].
基于声发射技术的Q345B疲劳裂纹扩展研究
[J].
Monitoring crack growth in pressure vessel steels by the acoustic emission technique and the method of potential difference
[J].
Acoustic emission monitoring for rolling contact fatigue of superfinished ground surfaces
[J].
Experimental study on the monitoring of crane steel beam fatigue characteristics with acoustic emission technology
[J].
起重机钢梁疲劳特性声发射监测实验研究
[J].
Acoustic emission testing on an F/A-18 E/F titanium bulkhead
[A].
Wideband and narrowband acoustic emission waveforms from extraneous sources during fatigue of steel samples
[J].
Structural reliability prediction using acoustic emission-based modeling of fatigue crack growth
[J].
Parameter analysis of acoustic emission signals
[J].
声发射信号的参数分析方法
[J].
A real-time approach to acoustic emission clustering
[J].
Effect of loading variables on the acoustic emissions of fatigue-crack growth
[J].
Acoustic emission during fatigue crack propagation in a micro-alloyed steel and welds
[J].
Effects of micro-structure on fatigue crack propagation and acoustic emission behaviors in a micro-alloyed steel
[J].
Influence of grain size on fatigue crack propagation and acoustic emission features in commercial-purity zirconium
[J].
Influence of micro structure on acoustic emission behavior during Stage 2 fatigue crack growth in solution annealed, thermally aged and weld specimens of AISI type 316 stainless steel
[J].
Acoustic emission detection of fatigue damage in cruciform welded joints
[J].
Acoustic emission assessment of through-thickness fatigue crack growth in steel members
[J].
Acoustic emission for fatigue damage characterization in metal plates
[J].
Acoustic emission energy as a fatigue damage parameter for CFRP composites
[J].
Effects of loading and sample geometry on acoustic emission generation during fatigue crack growth: implications for structural health monitoring
[J].
Fatigue cracks nucleation on steel, Acoustic emission and fractal analysis
[J].
Quantitative methods for structural health management using in situ acoustic emission monitoring
[J].
A Bayesian framework for structural health management using acoustic emission monitoring and periodic inspections
[D].
Probabilistic approach for nondestructive detection of fatigue crack initiation and sizing
[J].
Deterministic and probabilistic fatigue prognosis of cracked specimens using acoustic emissions
[J].
Application of chaos-based weak signal detection approach to the acoustic emission signal of gear crack via duffing oscillator
[J].
混沌弱信号检测法在齿轮裂纹声发射检测中的应用
[J].
Acoustic emission study of fatigue crack propagation in Q345R
[J].
Q345R疲劳裂纹扩展过程的声发射研究
[J].
Fatigue crack propagation of aluminum alloy based on acoustic emission monitoring
[J].
铝合金疲劳裂纹扩展声发射监测
[J].
Stable and unstable fatigue prediction for A572 structural steel using acoustic emission
[J].
Chaotic characteristics extracting and trend analysis on acoustic emission signal of tool condition
[J].
刀具声发射信号混沌特征提取及趋势分析
[J].
Analysis of acoustic emission signals in machining
[J].
Fault diagnosis of air compressor based on AE signals and correlation dimension
[J].
基于声发射和关联维数的空气压缩机故障诊断技术研究
[J].
Chaotic characteristic analysis of tool wear acoustic emission signal
[J].
Characteristic analysis and localization of acoustic emission source based on chaos theory
[J].
基于混沌理论的碰摩声发射特征分析与源定位
[J].根据混沌信号处理理论,研究分析了关联维数、最大Lyapunov指数和Kolmogorov熵等转子碰摩声发射源的非线性动力学特征量的特性。并将这些特征量作为神经网络的输入,研究了碰摩声发射源的定位问题。实验结果表明,该方法能较好地解决碰摩声发射源定位问题,为转子碰摩故障诊断提供依据。
Chaos analysis on acoustic emission signals of Francis turbine under cavitation
[J].
混流式水轮机空化声发射信号的混沌特性分析
[J].
Experimental Study on acoustic emission signals during glunting process of grinding wheels based on chaos theory
[J].
基于混沌理论砂轮磨钝过程声发射信号试验研究
[J].
Relevancy of correlation dimension and Kolmogorov entropy in state of gearbox discrimination
[J].
关联维数和Kolmogorov熵在变速箱状态判别中的关联性
[J].
Kolmogorov entropy diagnosis for vibration faults of turbine rotor based on wavelet packet filtering
[J].
基于小波包滤波的汽轮机转子振动故障的Kolmogorov熵诊断
[J].
Kolmogorov entropy and its application to the diagnosis of mechanical faults
[J].
柯尔莫哥洛夫熵及其在故障诊断中的应用
[J].
Estimation of the Kolmogorov entropy from a chaotic signal
[J].
Maximum-likelihood estimation of the entropy of an attractor
[J].
Chaos in thermal pulse combustion
[J].An experimental thermal pulse combustor and a differential equation model of this device are shown to exhibit chaotic behavior under certain conditions. Chaos arises in the model by means of a progression of period-doubling bifurcations that occur when operating parameters such as combustor wall temperature or air/fuel flow are adjusted to push the system toward flameout. Bifurcation sequences have not yet been reproduced experimentally, but similarities are demonstrated between the dynamic features of pressure fluctuations in the model and experiment. Correlation dimension, Kolmogorov entropy, and projections of reconstructed attractors using chaotic time series analysis are demonstrated to be useful in classifying dynamical behavior of the experimental combustor and for comparison of test data to the model results. Ways to improve the model are suggested. (c) 1995 American Institute of Physics.