Lateral deformation and defect resistance of compacted silica glass: quantification of the scratching hardness of brittle glasses
2
2018
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
... [1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
Evaluating abrasive wear of amorphous alloys using nanoscratch technique
3
2004
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
... 使用式(1)~(3)计算出的金属材料和聚合物PC的摩擦系数μcal,与表观摩擦系数曲线恒定阶段(取为最大载荷的70%~90%)的算术平均摩擦系数μavg基本相同(表2).因玻璃和陶瓷划痕的最大载荷较小(均小于10 N)压入深度较浅(小于d0),划痕过程一直处于圆球接触阶段,摩擦系数基本只由粘附摩擦系数构成,犁沟摩擦系数近似为零,计算出的摩擦系数也与μavg基本相同.这表明,三维力学接触模型能较为准确表征金属、玻璃、陶瓷和部分聚合物材料的摩擦系数.但是,金属玻璃的μavg小于计算得到的摩擦系数μcal.其原因是,金属玻璃的塑性变形由内部剪切带承担,剪切带的形核联接使阶段性出现磨损切削行为.金属玻璃的抗磨损性能表现出一定的特异性[2]. ...
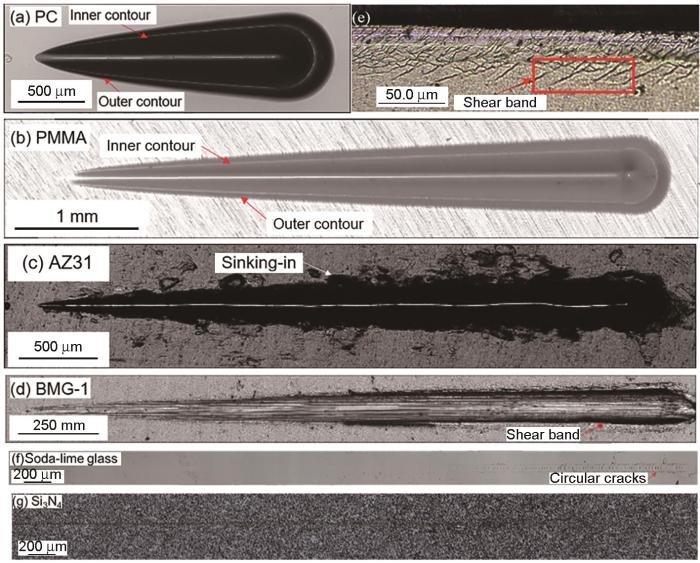
... 图7给出了六种材料(PC、PMMA、AZ31、BMG-1、soda-lime glass和Si3N4)划痕形貌的光学照片和BMG-1划痕沟槽边缘的局部放大图.随着压入载荷的增大材料的划痕宽度随之增大,但是不同类材料的划痕轮廓略有不同.两种聚合物材料(PMMA和PC)的划痕较为平滑清晰,可同时观察到内外两个划痕轮廓.内轮廓的产生是材料在划痕过程中堆积和下沉效应的结果(图1d),是聚合物材料特有的划痕现象[33].金属材料AZ31的划痕沟槽轮廓随着压入载荷的增大而表现为锯齿状,是划痕时材料的剪切流动和堆积撕裂造成的[10].BMG-1的划痕轮廓比金属材料AZ31更为平滑,在载荷较大时产生微裂纹或剪切带[2].soda-lime glass和Si3N4的硬度和弹性模量较大而施加的载荷较小,因此在光学照片中划痕沟槽并不明显.在载荷较小(10 N)的情况下在soda-lime glass划痕末端仍产生了圆型裂纹,是其断裂韧性较小(0.75 MPa·m1/2)所致.可以看出,Si3N4试样的表面并不光滑,因为其有很大的不均匀性.这从切向力Ft和摩擦系数μapp随载荷Fn的变化(图4f)中也可看出. ...
Scratch behavior of polycarbonate by Rockwell C diamond indenter under progressive loading
3
2020
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
... Liu在Akono和Hubler等研究结果的基础上提出一个断裂韧性分析模型[3] ...
Material specific nanoscratch ploughing friction coefficient
1
2018
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
Experimental determination of the fracture toughness via microscratch tests: application to polymers, ceramics, and metals
4
2012
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
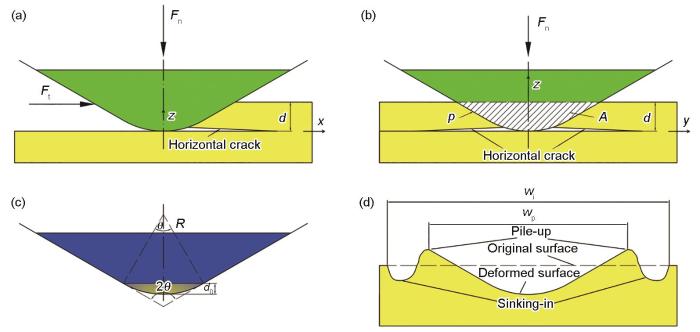
... 可根据断裂准则推出[5].式中Ft为划痕过程中记录的切向力,p为压头与试样接触部分在划痕方向上的投影周长,A为压头与试样接触部分在划痕方向上的投影面积(图1b).在载荷较小的初始阶段只有压头尖端的圆球部分与试样接触,可认为是圆球形压头的划痕模式.随着压入载荷的增大压入深度超过压头球-锥部分临界深度d0,划痕模式转变为球-锥混合划痕模式.由几何关系(图1b-c)可知,在递增载荷下的划痕过程中压头与试样接触部分在划痕方向上的投影面积A和投影周长p可以表示为[17] ...
... 四种模型的适用有一定的材料范围,因为各种基于线弹性断裂力学和微观能量尺寸效应定律的模型需要使材料达到由塑性屈服到断裂的临界状态,这对于断裂韧性较大的材料而言需要相当大的压入载荷,甚至超过微米划痕仪的最大载荷(30 N)[5]. ...
Size-effect law for scratch tests of axisymmetric shape
2
2016
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
... Hubler和Ulm等根据准脆性材料的断裂能量尺寸定律,提出了另一种断裂韧性评估模型[6] ...
Energetic size effect law at the microscopic scale: application to progressive-load scratch testing
4
2016
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
... Akono等根据微观能量尺寸效应定律提出[7] ...
... 其中为材料的名义应力,为名义尺寸,为与材料有关的常数.名义尺寸又可表示为[7] ...
Abrasion resistance of lamellar graphite iron: interaction between microstructure and abrasive particles
3
2018
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
... 划痕宽度可用来计算划痕硬度.划痕硬度可用于评估材料的耐磨性.与压痕硬度相比,划痕硬度更能反映划痕时一定体积材料产生塑性变形所需的功[34].在完全塑性材料的划痕过程中压头施加的法向载荷完全由压头前锥面下的材料承受,因此与压痕实验相比在同等载荷下压头会压入得更深,直至压头前锥面的接触面积达到相同的压痕接触面积.而对于纯弹性材料,由于划痕过程中压头后锥面材料瞬间恢复,压头施加的法向载荷由前后锥面共同承受,在压入深度方向材料产生与压痕实验相同的变形[8].大多数弹塑性材料的划痕变形行为处于这两者之间,这种划痕变形行为与材料的弹性恢复率[35]和实验采用的划痕速度[36]有关.材料的划痕硬度定义为[37] ...
... 图10给出了用公式(5)计算的划痕硬度随压入载荷的关系.可以看出,压入载荷较小时四种材料的划痕硬度均随着压入载荷的增大而减小.这个结果,与Ghasemi等[8]在片状石墨铸铁的划痕实验中观察到的现象一致.其原因是,压入深度较小时材料的弹性变形的比重较大.随着压入载荷的增大,划痕硬度逐渐增加并趋向于稳定.同时,AZ31的硬度曲线在稳定段出现一定幅度的波动,与划痕过程中的下沉效应有关.所有材料在划痕硬度曲线稳定段的算术平均值,列于表2. ...
Glass fracture during micro-scratching
1
2020
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
Measurement of fracture toughness of copper via constant-load microscratch with a spherical indenter
2
2020
... 微米划痕技术,是一种使用压头在试样表面进行微米划刻以得到材料(玻璃[1]、金属[2]和聚合物[3]等)力学参数的方法.制备微米划痕用试样较为简单且对其没有较大的损伤,因此广泛用于研究材料的摩擦磨损[4]、划痕硬度[1]和断裂韧性[5-7]等力学性能.微米划痕技术有恒定载荷和递增载荷两种加载模式,用递增载荷模式可研究在单次划痕实验中加载力对试样划痕变形机制的影响[8].脆性材料(如玻璃和陶瓷等)在小力下划痕时其沟槽边缘会出现裂纹和碎屑[9],而大部分韧性材料(如金属和聚合物等)通常出现较剧烈的堆积和下沉[10].不同材料的划痕行为,因其微观结构和变形机理的影响而有较大的不同.进行递增载荷下的微米划痕实验从微观角度研究材料的力学性能和变形机制,有助于发现不同类材料力学性能间的内在联系并为材料的加工成型提供理论指导. ...
... 图7给出了六种材料(PC、PMMA、AZ31、BMG-1、soda-lime glass和Si3N4)划痕形貌的光学照片和BMG-1划痕沟槽边缘的局部放大图.随着压入载荷的增大材料的划痕宽度随之增大,但是不同类材料的划痕轮廓略有不同.两种聚合物材料(PMMA和PC)的划痕较为平滑清晰,可同时观察到内外两个划痕轮廓.内轮廓的产生是材料在划痕过程中堆积和下沉效应的结果(图1d),是聚合物材料特有的划痕现象[33].金属材料AZ31的划痕沟槽轮廓随着压入载荷的增大而表现为锯齿状,是划痕时材料的剪切流动和堆积撕裂造成的[10].BMG-1的划痕轮廓比金属材料AZ31更为平滑,在载荷较大时产生微裂纹或剪切带[2].soda-lime glass和Si3N4的硬度和弹性模量较大而施加的载荷较小,因此在光学照片中划痕沟槽并不明显.在载荷较小(10 N)的情况下在soda-lime glass划痕末端仍产生了圆型裂纹,是其断裂韧性较小(0.75 MPa·m1/2)所致.可以看出,Si3N4试样的表面并不光滑,因为其有很大的不均匀性.这从切向力Ft和摩擦系数μapp随载荷Fn的变化(图4f)中也可看出. ...
The fracture toughness of bulk metallic glasses
1
2010
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
On the fracture toughness of bulk metallic glasses under Berkovich nanoindentation
1
2018
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
利用维式和玻式压头表征半导体材料断裂韧性
1
2021
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
利用维式和玻式压头表征半导体材料断裂韧性
1
2021
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
Measurement of fracture toughness by nanoindentation methods: recent advances and future challenges
1
2015
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
高强钢断裂韧性KIC的小尺寸试样评价方法
1
2018
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
高强钢断裂韧性KIC的小尺寸试样评价方法
1
2018
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
Can scratch tests give fracture toughness?
1
2013
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
利用圆锥压头微米划痕测试材料断裂韧性
6
2019
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... [
17]
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 可根据断裂准则推出[5].式中Ft为划痕过程中记录的切向力,p为压头与试样接触部分在划痕方向上的投影周长,A为压头与试样接触部分在划痕方向上的投影面积(图1b).在载荷较小的初始阶段只有压头尖端的圆球部分与试样接触,可认为是圆球形压头的划痕模式.随着压入载荷的增大压入深度超过压头球-锥部分临界深度d0,划痕模式转变为球-锥混合划痕模式.由几何关系(图1b-c)可知,在递增载荷下的划痕过程中压头与试样接触部分在划痕方向上的投影面积A和投影周长p可以表示为[17] ...
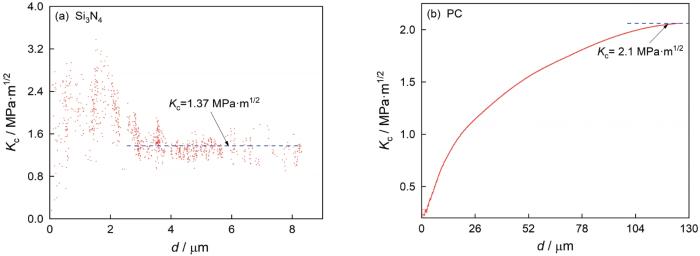
... 基于LEFM模型的断裂韧性分析,如图13所示.材料在达到裂纹失稳时的实验数据才可用于LEFM模型,因此较大载荷下的曲线平稳段才真正反映断裂韧性值.图13a中Si3N4在断裂韧性曲线平稳段的平均值为1.37 MPa·m1/2,与前人所得断裂韧性1.26 MPa·m1/2基本一致[40].图13b中PC在断裂韧性曲线平稳段的平均值为2.1 MPa·m1/2,与前人[17]所得断裂韧性2.2 MPa·m1/2一致.基于LEFM模型得到的所有材料的断裂韧性值Kc,列于表3.表3还列出了前人用传统方法(三点弯曲、紧凑拉伸和压痕法)得到的断裂韧性值.从表3可见,(紫铜和BMG-3),LEFM模型均能准确表征玻璃、陶瓷、聚合物和部分金属和金属玻璃材料的断裂韧性,得到的值与传统方法一致. ...
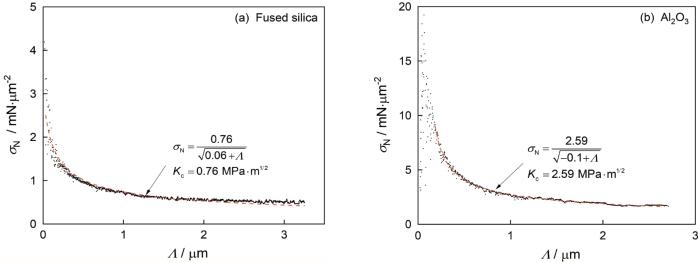
... 图14给出了用Akono’s MESEL模型对Fused silica和Al2O3的断裂韧性分析结果.此模型能很好拟合实验数据(相关系数大于0.9),得到的Fused silica和Al2O3的断裂韧性分别为0.76 MPa·m1/2和2.59 MPa·m1/2,与前人所得结果0.8 MPa·m1/2 [17]和2.346 MPa·m1/2 [41]相当接近.这表明,Akono’s MESEL模型能很好地表征材料的断裂韧性.根据Akono’s MESEL模型所得断裂韧性值与根据LEFM模型所得结果基本一致,但是不能准确表征大部分断裂韧性较大的材料(例如AZ31、钼、钨和部分非晶合金). ...
利用圆锥压头微米划痕测试材料断裂韧性
6
2019
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... [
17]
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 可根据断裂准则推出[5].式中Ft为划痕过程中记录的切向力,p为压头与试样接触部分在划痕方向上的投影周长,A为压头与试样接触部分在划痕方向上的投影面积(图1b).在载荷较小的初始阶段只有压头尖端的圆球部分与试样接触,可认为是圆球形压头的划痕模式.随着压入载荷的增大压入深度超过压头球-锥部分临界深度d0,划痕模式转变为球-锥混合划痕模式.由几何关系(图1b-c)可知,在递增载荷下的划痕过程中压头与试样接触部分在划痕方向上的投影面积A和投影周长p可以表示为[17] ...
... 基于LEFM模型的断裂韧性分析,如图13所示.材料在达到裂纹失稳时的实验数据才可用于LEFM模型,因此较大载荷下的曲线平稳段才真正反映断裂韧性值.图13a中Si3N4在断裂韧性曲线平稳段的平均值为1.37 MPa·m1/2,与前人所得断裂韧性1.26 MPa·m1/2基本一致[40].图13b中PC在断裂韧性曲线平稳段的平均值为2.1 MPa·m1/2,与前人[17]所得断裂韧性2.2 MPa·m1/2一致.基于LEFM模型得到的所有材料的断裂韧性值Kc,列于表3.表3还列出了前人用传统方法(三点弯曲、紧凑拉伸和压痕法)得到的断裂韧性值.从表3可见,(紫铜和BMG-3),LEFM模型均能准确表征玻璃、陶瓷、聚合物和部分金属和金属玻璃材料的断裂韧性,得到的值与传统方法一致. ...
... 图14给出了用Akono’s MESEL模型对Fused silica和Al2O3的断裂韧性分析结果.此模型能很好拟合实验数据(相关系数大于0.9),得到的Fused silica和Al2O3的断裂韧性分别为0.76 MPa·m1/2和2.59 MPa·m1/2,与前人所得结果0.8 MPa·m1/2 [17]和2.346 MPa·m1/2 [41]相当接近.这表明,Akono’s MESEL模型能很好地表征材料的断裂韧性.根据Akono’s MESEL模型所得断裂韧性值与根据LEFM模型所得结果基本一致,但是不能准确表征大部分断裂韧性较大的材料(例如AZ31、钼、钨和部分非晶合金). ...
利用微米划痕研究TiN涂层的失效机理
1
2020
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
利用微米划痕研究TiN涂层的失效机理
1
2020
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
Sliding of a diamond sphere on fused silica under ramping load
1
2020
... 断裂韧性是评估材料完整性的重要参数,体现材料对裂纹扩展的抵抗能力[11].进行单边开缺口的三点弯曲实验或紧凑拉伸实验,根据裂纹尖端的张开位移可计算材料的断裂韧性.但是,这些方法对试样的几何形状和尺寸十分敏感[12,13],且预制疲劳裂纹和裂纹的长度都难以控制[14].寻求一种简单且可靠的材料断裂韧性测试方式,成为当下研究的热点[15].用微米划痕技术测试材料的断裂韧性,可避免试样制备的繁琐且不需要测量裂纹长度,减小了主观误差.Akono等[5]基于线弹性断裂力学(LEFM)理论,利用划痕过程中侧向力与压头形函数的幂律关系可测出材料的断裂韧性.而Lin等[16]认为,划痕深度较小时LEFM模型并不能准确表征材料的断裂韧性.因制造工艺的约束,圆锥型压头的尖端并不简单收敛于一点而是呈圆球形状,压头上有一个圆锥与圆球阶段的过渡区域,因此不能用单一的幂律式描述圆锥型压头的形函数.修正压头形函数前后,使用LEFM模型得出的断裂韧性有较大的差异[17,18].同时,Akono[7]、Hubler[6]和Liu[3]等根据微观能量尺寸效应(MESEL)理论也分别提出了基于量纲分析的断裂韧性评估模型.但是,与不适用于低泊松比材料的压痕方法类似[19],这些划痕断裂韧性模型是否适用于所有类型的材料仍需进一步探讨. ...
基于水平集方法的划痕形状表面视觉测量
2
2020
... 划痕实验:先用5 mN的极小恒定载荷对试样进行预扫描探测试样表面形貌;然后压头以设定的加载方式进行划刻实验,得到压入深度d和切向力Ft;最后压头以5 mN的恒定载荷对划痕进行后扫描,得到划痕沟槽的残余深度dr.用光学显微镜对划痕形貌拍照并全景成像.使用图像处理软件[20]对划痕图像进行划痕沟槽的提取分析.用显微硬度计MHVKD-1000测试16种材料的努氏硬度,所用金刚石努氏压头是两棱间半夹角分别为86°25′和65°的四棱锥[21].在努氏压痕实验中所有试样的保载时间均为15 s,所用载荷P和得到的努氏硬度Hi分别列于表1和表2. ...
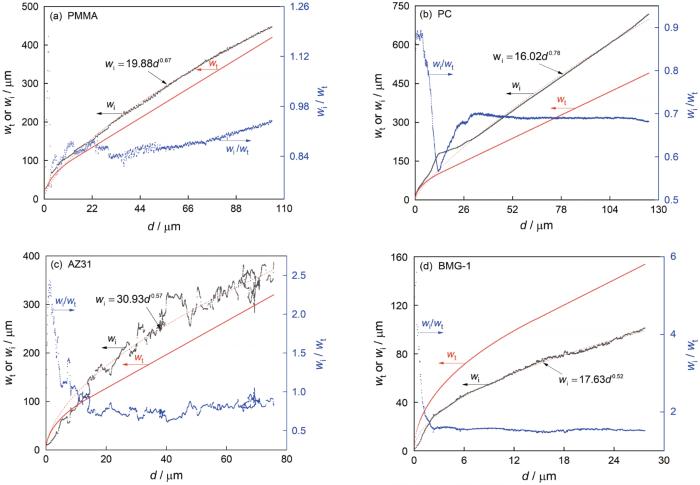
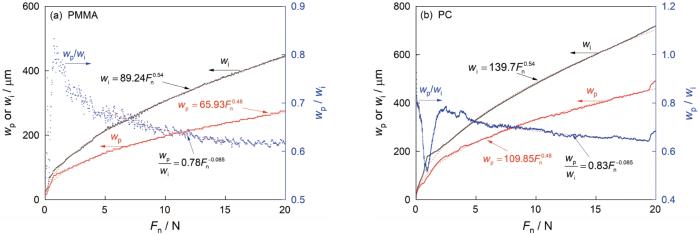
... 为了研究材料的实际划痕宽度与压入载荷和压入深度的关系,使用划痕图像分析软件[20]提取了划痕轮廓,以进一步分析材料的弹塑性划痕行为.图8给出了四种材料的理论计算宽度wt和实际测量宽度wi随压入深度d的变化,其中两种聚合物的实际宽度是从外轮廓中提取的.玻璃和陶瓷的划痕载荷较小,划痕有较大的弹性恢复(划痕保持率几乎为零).光学照片中的划痕轮廓较难识别测量,因此没有定量分析划痕的实际宽度.图8除金属玻璃BMG-1外,其余材料的实际划痕宽度均略大于理论宽度.这表明,划痕轮廓边缘出现了较为严重的材料堆积.这种堆积效应,与材料的塑性有关.BMG-1的这种特异性,主要源于其较大的弹性恢复,这种情况在压入深度较小(相对其他三种材料)时更为明显.压入深度较小时压头与材料之间以弹性接触为主,塑性变形部分较小,划痕的实际宽度与理论宽度近似相同.随着压入深度的增加,理论宽度偏离实际宽度.为了描述这种偏离程度,引入了宽度保持率wi/wt.从图8可见,压入深度较大时宽度保持率均趋于恒定,PMMA材料在接近最大载荷时宽度保持率略有提高,因为沟槽末端的堆积效应较为显著. ...
基于水平集方法的划痕形状表面视觉测量
2
2020
... 划痕实验:先用5 mN的极小恒定载荷对试样进行预扫描探测试样表面形貌;然后压头以设定的加载方式进行划刻实验,得到压入深度d和切向力Ft;最后压头以5 mN的恒定载荷对划痕进行后扫描,得到划痕沟槽的残余深度dr.用光学显微镜对划痕形貌拍照并全景成像.使用图像处理软件[20]对划痕图像进行划痕沟槽的提取分析.用显微硬度计MHVKD-1000测试16种材料的努氏硬度,所用金刚石努氏压头是两棱间半夹角分别为86°25′和65°的四棱锥[21].在努氏压痕实验中所有试样的保载时间均为15 s,所用载荷P和得到的努氏硬度Hi分别列于表1和表2. ...
... 为了研究材料的实际划痕宽度与压入载荷和压入深度的关系,使用划痕图像分析软件[20]提取了划痕轮廓,以进一步分析材料的弹塑性划痕行为.图8给出了四种材料的理论计算宽度wt和实际测量宽度wi随压入深度d的变化,其中两种聚合物的实际宽度是从外轮廓中提取的.玻璃和陶瓷的划痕载荷较小,划痕有较大的弹性恢复(划痕保持率几乎为零).光学照片中的划痕轮廓较难识别测量,因此没有定量分析划痕的实际宽度.图8除金属玻璃BMG-1外,其余材料的实际划痕宽度均略大于理论宽度.这表明,划痕轮廓边缘出现了较为严重的材料堆积.这种堆积效应,与材料的塑性有关.BMG-1的这种特异性,主要源于其较大的弹性恢复,这种情况在压入深度较小(相对其他三种材料)时更为明显.压入深度较小时压头与材料之间以弹性接触为主,塑性变形部分较小,划痕的实际宽度与理论宽度近似相同.随着压入深度的增加,理论宽度偏离实际宽度.为了描述这种偏离程度,引入了宽度保持率wi/wt.从图8可见,压入深度较大时宽度保持率均趋于恒定,PMMA材料在接近最大载荷时宽度保持率略有提高,因为沟槽末端的堆积效应较为显著. ...
基于努氏硬度表征大块金属玻璃的力学性能
1
2021
... 划痕实验:先用5 mN的极小恒定载荷对试样进行预扫描探测试样表面形貌;然后压头以设定的加载方式进行划刻实验,得到压入深度d和切向力Ft;最后压头以5 mN的恒定载荷对划痕进行后扫描,得到划痕沟槽的残余深度dr.用光学显微镜对划痕形貌拍照并全景成像.使用图像处理软件[20]对划痕图像进行划痕沟槽的提取分析.用显微硬度计MHVKD-1000测试16种材料的努氏硬度,所用金刚石努氏压头是两棱间半夹角分别为86°25′和65°的四棱锥[21].在努氏压痕实验中所有试样的保载时间均为15 s,所用载荷P和得到的努氏硬度Hi分别列于表1和表2. ...
基于努氏硬度表征大块金属玻璃的力学性能
1
2021
... 划痕实验:先用5 mN的极小恒定载荷对试样进行预扫描探测试样表面形貌;然后压头以设定的加载方式进行划刻实验,得到压入深度d和切向力Ft;最后压头以5 mN的恒定载荷对划痕进行后扫描,得到划痕沟槽的残余深度dr.用光学显微镜对划痕形貌拍照并全景成像.使用图像处理软件[20]对划痕图像进行划痕沟槽的提取分析.用显微硬度计MHVKD-1000测试16种材料的努氏硬度,所用金刚石努氏压头是两棱间半夹角分别为86°25′和65°的四棱锥[21].在努氏压痕实验中所有试样的保载时间均为15 s,所用载荷P和得到的努氏硬度Hi分别列于表1和表2. ...
AZ31镁合金变路径压缩的力学性能和孪晶机制
1
2016
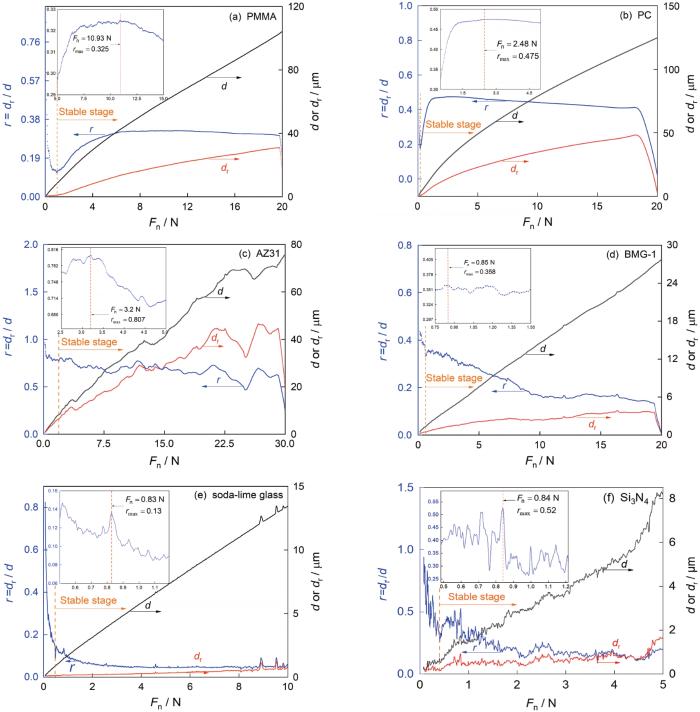
... 图2给出了六种材料的压入深度和残余深度与压入载荷的关系.可以看出,压入深度d和残余深度dr都随着压入载荷Fn的增大而增大,但是其变化幅度不同,因为其弹性恢复不同.压入载荷接近预设最大载荷时,除玻璃和陶瓷材料外的材料残余深度曲线都急剧下降.其原因是,在划痕沟槽的末端发生了较严重的材料堆积和回弹,而玻璃和陶瓷材料的塑性变形较小,没有出现严重的堆积.密排六方结构的镁合金AZ31其载荷-深度曲线剧烈波动,因为在室温下塑性变形主要由晶面滑移和孪晶承担,变形过程中孪晶界的形核阻碍了位错运动,使后续二次孪晶对应的屈服强度大幅度提高[22],导致压入深度曲线呈阶梯式增长.与其他类材料相比,玻璃soda-lime glass和陶瓷Si3N4的压入深度和残余深度都较小,因为其硬度和弹性模量都比较高.为了更好地描述这种弹性恢复随压入载荷的变化,引入划痕保持率r=dr/d以分析划痕的回弹行为.划痕保持率曲线初期的减小源于试样表面粗糙度的影响,进入划痕的稳定阶段后随着压入载荷的增大划痕保持率先增大后减小.存在局部最大划痕保持率rmax,因为划痕保持率是划痕过程中弹性变形与塑性变形两种变形机制竞争的结果. ...
AZ31镁合金变路径压缩的力学性能和孪晶机制
1
2016
... 图2给出了六种材料的压入深度和残余深度与压入载荷的关系.可以看出,压入深度d和残余深度dr都随着压入载荷Fn的增大而增大,但是其变化幅度不同,因为其弹性恢复不同.压入载荷接近预设最大载荷时,除玻璃和陶瓷材料外的材料残余深度曲线都急剧下降.其原因是,在划痕沟槽的末端发生了较严重的材料堆积和回弹,而玻璃和陶瓷材料的塑性变形较小,没有出现严重的堆积.密排六方结构的镁合金AZ31其载荷-深度曲线剧烈波动,因为在室温下塑性变形主要由晶面滑移和孪晶承担,变形过程中孪晶界的形核阻碍了位错运动,使后续二次孪晶对应的屈服强度大幅度提高[22],导致压入深度曲线呈阶梯式增长.与其他类材料相比,玻璃soda-lime glass和陶瓷Si3N4的压入深度和残余深度都较小,因为其硬度和弹性模量都比较高.为了更好地描述这种弹性恢复随压入载荷的变化,引入划痕保持率r=dr/d以分析划痕的回弹行为.划痕保持率曲线初期的减小源于试样表面粗糙度的影响,进入划痕的稳定阶段后随着压入载荷的增大划痕保持率先增大后减小.存在局部最大划痕保持率rmax,因为划痕保持率是划痕过程中弹性变形与塑性变形两种变形机制竞争的结果. ...
Characterization on the yield stress and interfacial coefficient of friction of glasses from scratch tests
1
2020
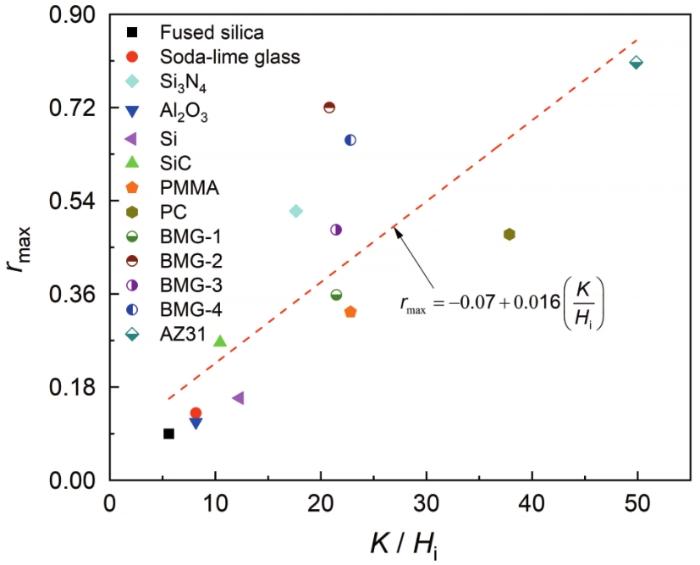
... 图3给出了划痕稳定阶段的最大划痕保持率rmax与体积模量K和压痕硬度Hi的比值(K/Hi)之间的关系.实验结果表明,这两种参数的关系是线性的.文献中材料的体积模量K列于表2.最大划痕保持率rmax随K/Hi增大而增大,因为最大划痕保持率rmax与材料本身的弹塑性性能有关[23],而体积模量与压痕硬度分别表征了材料的弹性和抗塑性变形能力.因此,体积模量和压痕硬度的比值(K/Hi)会与最大划痕保持率rmax有一定的联系. ...
Tribology behavior during indentation and scratch of thin films on substrates: effects of plastic friction
2
2015
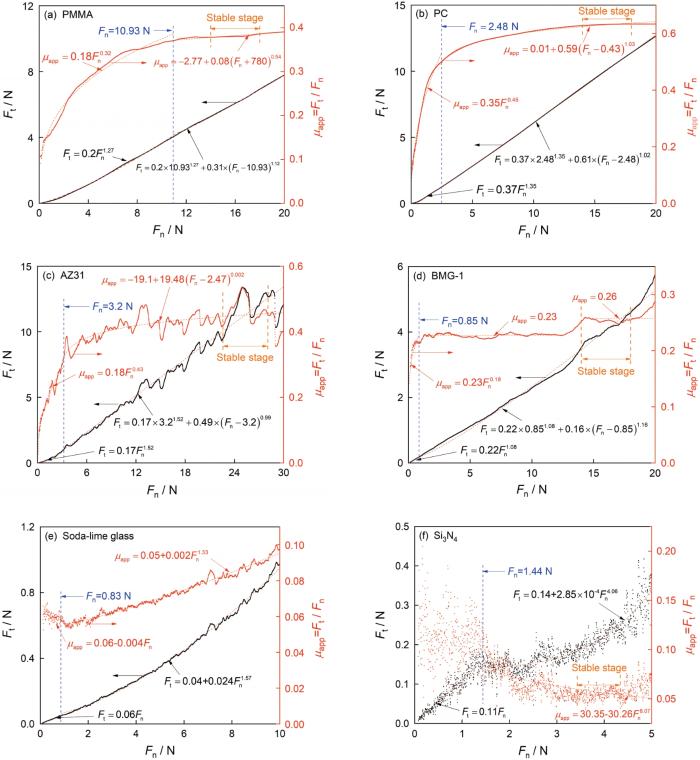
... 可用三维力学接触模型表征表观摩擦系数曲线恒定阶段的算术平均值μavg,按照三维力学接触模型计算出的摩擦系数可表示为[24] ...
... 其中μadh为黏着摩擦系数,μdef为犁沟摩擦系数.黏着摩擦系数越大,划痕的堆积越显著[24].当压入深度很小而只有压头尖端的圆球部分与试样接触时,表明已经处于完全弹性接触阶段,可使用三维接触力学模型计算材料的黏着摩擦系数[25] ...
A surface flow line model of a scratching tip: apparent and true local friction coefficients
2
2004
... 其中μadh为黏着摩擦系数,μdef为犁沟摩擦系数.黏着摩擦系数越大,划痕的堆积越显著[24].当压入深度很小而只有压头尖端的圆球部分与试样接触时,表明已经处于完全弹性接触阶段,可使用三维接触力学模型计算材料的黏着摩擦系数[25] ...
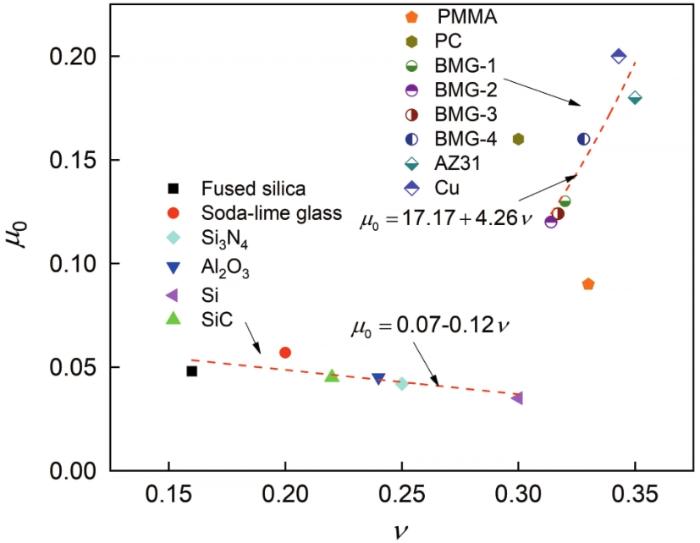
... 图5给出了材料的初始摩擦系数μ0与泊松比v之间的关系.可以看出,材料的初始摩擦系数与泊松比并无单一的联系,但是在泊松比为0.3的两侧都表现出一定的线性关系.在泊松比小于0.3的左侧为硬脆材料(玻璃和陶瓷),大于0.3的右侧的为韧性材料(金属和金属玻璃).其原因是,材料的初始摩擦系数与黏着摩擦系数密切相关(式2),而黏着摩擦系数决定于材料的硬脆性[25].除了硬度,材料的磨损性能还与断裂韧性有关,泊松比则在一定程度上反映了材料的断裂韧性[28],因为材料的塑性流动和断裂行为与弹性性能密切相关[29].聚合物(PMMA和PC)的变形能力取决于其分子链的滑动和拉扯以及链的旋转[30],因此其弹塑性变形行为受多种因素(温度、划痕速度等[31])影响,从而使其初始摩擦系数不服从线性规律. ...
法向载荷对紫铜的微米划痕测试的影响
1
2020
... 压头压入较软材料后在滑动中推挤材料,产生塑性流动并划出一条沟槽(称为犁沟).所受滑动阻力与压入载荷的比值,称为犁沟摩擦系数[26].随着压入载荷的增大,表观摩擦系数均先增大然后趋于稳定.在只考虑犁沟行为不考虑材料弹性恢复的情况下,圆锥形压头在划痕过程中只有压头的前半部分与材料接触,犁沟摩擦系数只与压头形状有关且为一恒定值,可表示为[27] ...
法向载荷对紫铜的微米划痕测试的影响
1
2020
... 压头压入较软材料后在滑动中推挤材料,产生塑性流动并划出一条沟槽(称为犁沟).所受滑动阻力与压入载荷的比值,称为犁沟摩擦系数[26].随着压入载荷的增大,表观摩擦系数均先增大然后趋于稳定.在只考虑犁沟行为不考虑材料弹性恢复的情况下,圆锥形压头在划痕过程中只有压头的前半部分与材料接触,犁沟摩擦系数只与压头形状有关且为一恒定值,可表示为[27] ...
Analytical model of friction behavior during polymer scratching with conical tip
1
2019
... 压头压入较软材料后在滑动中推挤材料,产生塑性流动并划出一条沟槽(称为犁沟).所受滑动阻力与压入载荷的比值,称为犁沟摩擦系数[26].随着压入载荷的增大,表观摩擦系数均先增大然后趋于稳定.在只考虑犁沟行为不考虑材料弹性恢复的情况下,圆锥形压头在划痕过程中只有压头的前半部分与材料接触,犁沟摩擦系数只与压头形状有关且为一恒定值,可表示为[27] ...
Correlations between the wear resistance and properties of bulk metallic glasses
2
2018
... 图5给出了材料的初始摩擦系数μ0与泊松比v之间的关系.可以看出,材料的初始摩擦系数与泊松比并无单一的联系,但是在泊松比为0.3的两侧都表现出一定的线性关系.在泊松比小于0.3的左侧为硬脆材料(玻璃和陶瓷),大于0.3的右侧的为韧性材料(金属和金属玻璃).其原因是,材料的初始摩擦系数与黏着摩擦系数密切相关(式2),而黏着摩擦系数决定于材料的硬脆性[25].除了硬度,材料的磨损性能还与断裂韧性有关,泊松比则在一定程度上反映了材料的断裂韧性[28],因为材料的塑性流动和断裂行为与弹性性能密切相关[29].聚合物(PMMA和PC)的变形能力取决于其分子链的滑动和拉扯以及链的旋转[30],因此其弹塑性变形行为受多种因素(温度、划痕速度等[31])影响,从而使其初始摩擦系数不服从线性规律. ...
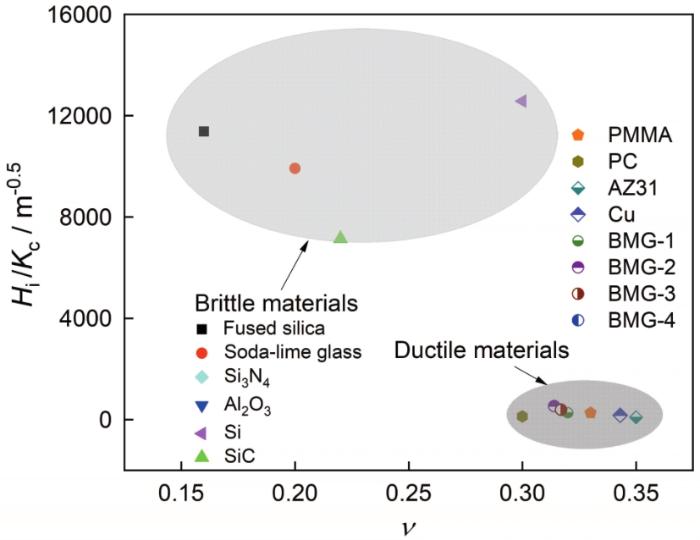
... 图6给出了材料的脆性指数(压痕硬度Hi与断裂韧性Kc的比值,Hi/Kc)与泊松比v之间的关系.所有材料的断裂韧性值Kc列于表3.脆性指数体现了材料受力变形时塑性变形与裂纹扩展的竞争[32],脆性指数越大表明材料越‘脆’.图6表明,玻璃和陶瓷材料的脆性指数是聚合物和金属材料的近千倍,泊松比为0.3处可作为脆-韧材料区域的分界点.与图5对应,脆性材料区和韧性材料区各自呈现初始摩擦系数与泊松比的线性规律.其原因是,脆性材料的磨损性能由断裂韧性主导,而韧性材料的磨损性能更取决于材料的硬度,其磨损机制不同[28].同时,泊松比同为0.3的Si和PC材料其脆性指数却相差很大.这表明,弹性参数泊松比只能粗略评估材料的韧脆性. ...
The elastic properties, elastic models and elastic perspectives of metallic glasses
1
2012
... 图5给出了材料的初始摩擦系数μ0与泊松比v之间的关系.可以看出,材料的初始摩擦系数与泊松比并无单一的联系,但是在泊松比为0.3的两侧都表现出一定的线性关系.在泊松比小于0.3的左侧为硬脆材料(玻璃和陶瓷),大于0.3的右侧的为韧性材料(金属和金属玻璃).其原因是,材料的初始摩擦系数与黏着摩擦系数密切相关(式2),而黏着摩擦系数决定于材料的硬脆性[25].除了硬度,材料的磨损性能还与断裂韧性有关,泊松比则在一定程度上反映了材料的断裂韧性[28],因为材料的塑性流动和断裂行为与弹性性能密切相关[29].聚合物(PMMA和PC)的变形能力取决于其分子链的滑动和拉扯以及链的旋转[30],因此其弹塑性变形行为受多种因素(温度、划痕速度等[31])影响,从而使其初始摩擦系数不服从线性规律. ...
Positron lifetime spectroscopy characterization of thermal history effects on polycarbonate
1
1990
... 图5给出了材料的初始摩擦系数μ0与泊松比v之间的关系.可以看出,材料的初始摩擦系数与泊松比并无单一的联系,但是在泊松比为0.3的两侧都表现出一定的线性关系.在泊松比小于0.3的左侧为硬脆材料(玻璃和陶瓷),大于0.3的右侧的为韧性材料(金属和金属玻璃).其原因是,材料的初始摩擦系数与黏着摩擦系数密切相关(式2),而黏着摩擦系数决定于材料的硬脆性[25].除了硬度,材料的磨损性能还与断裂韧性有关,泊松比则在一定程度上反映了材料的断裂韧性[28],因为材料的塑性流动和断裂行为与弹性性能密切相关[29].聚合物(PMMA和PC)的变形能力取决于其分子链的滑动和拉扯以及链的旋转[30],因此其弹塑性变形行为受多种因素(温度、划痕速度等[31])影响,从而使其初始摩擦系数不服从线性规律. ...
The mechanism of creep behaviour in glassy polymers
1
1975
... 图5给出了材料的初始摩擦系数μ0与泊松比v之间的关系.可以看出,材料的初始摩擦系数与泊松比并无单一的联系,但是在泊松比为0.3的两侧都表现出一定的线性关系.在泊松比小于0.3的左侧为硬脆材料(玻璃和陶瓷),大于0.3的右侧的为韧性材料(金属和金属玻璃).其原因是,材料的初始摩擦系数与黏着摩擦系数密切相关(式2),而黏着摩擦系数决定于材料的硬脆性[25].除了硬度,材料的磨损性能还与断裂韧性有关,泊松比则在一定程度上反映了材料的断裂韧性[28],因为材料的塑性流动和断裂行为与弹性性能密切相关[29].聚合物(PMMA和PC)的变形能力取决于其分子链的滑动和拉扯以及链的旋转[30],因此其弹塑性变形行为受多种因素(温度、划痕速度等[31])影响,从而使其初始摩擦系数不服从线性规律. ...
Surface damage of soda-lime-silica glasses: indentation scratch behavior
1
2003
... 图6给出了材料的脆性指数(压痕硬度Hi与断裂韧性Kc的比值,Hi/Kc)与泊松比v之间的关系.所有材料的断裂韧性值Kc列于表3.脆性指数体现了材料受力变形时塑性变形与裂纹扩展的竞争[32],脆性指数越大表明材料越‘脆’.图6表明,玻璃和陶瓷材料的脆性指数是聚合物和金属材料的近千倍,泊松比为0.3处可作为脆-韧材料区域的分界点.与图5对应,脆性材料区和韧性材料区各自呈现初始摩擦系数与泊松比的线性规律.其原因是,脆性材料的磨损性能由断裂韧性主导,而韧性材料的磨损性能更取决于材料的硬度,其磨损机制不同[28].同时,泊松比同为0.3的Si和PC材料其脆性指数却相差很大.这表明,弹性参数泊松比只能粗略评估材料的韧脆性. ...
Finite element method parametric study on scratch behavior of polymers
1
2010
... 图7给出了六种材料(PC、PMMA、AZ31、BMG-1、soda-lime glass和Si3N4)划痕形貌的光学照片和BMG-1划痕沟槽边缘的局部放大图.随着压入载荷的增大材料的划痕宽度随之增大,但是不同类材料的划痕轮廓略有不同.两种聚合物材料(PMMA和PC)的划痕较为平滑清晰,可同时观察到内外两个划痕轮廓.内轮廓的产生是材料在划痕过程中堆积和下沉效应的结果(图1d),是聚合物材料特有的划痕现象[33].金属材料AZ31的划痕沟槽轮廓随着压入载荷的增大而表现为锯齿状,是划痕时材料的剪切流动和堆积撕裂造成的[10].BMG-1的划痕轮廓比金属材料AZ31更为平滑,在载荷较大时产生微裂纹或剪切带[2].soda-lime glass和Si3N4的硬度和弹性模量较大而施加的载荷较小,因此在光学照片中划痕沟槽并不明显.在载荷较小(10 N)的情况下在soda-lime glass划痕末端仍产生了圆型裂纹,是其断裂韧性较小(0.75 MPa·m1/2)所致.可以看出,Si3N4试样的表面并不光滑,因为其有很大的不均匀性.这从切向力Ft和摩擦系数μapp随载荷Fn的变化(图4f)中也可看出. ...
Scratch hardness of glass
2
2018
... 划痕宽度可用来计算划痕硬度.划痕硬度可用于评估材料的耐磨性.与压痕硬度相比,划痕硬度更能反映划痕时一定体积材料产生塑性变形所需的功[34].在完全塑性材料的划痕过程中压头施加的法向载荷完全由压头前锥面下的材料承受,因此与压痕实验相比在同等载荷下压头会压入得更深,直至压头前锥面的接触面积达到相同的压痕接触面积.而对于纯弹性材料,由于划痕过程中压头后锥面材料瞬间恢复,压头施加的法向载荷由前后锥面共同承受,在压入深度方向材料产生与压痕实验相同的变形[8].大多数弹塑性材料的划痕变形行为处于这两者之间,这种划痕变形行为与材料的弹性恢复率[35]和实验采用的划痕速度[36]有关.材料的划痕硬度定义为[37] ...
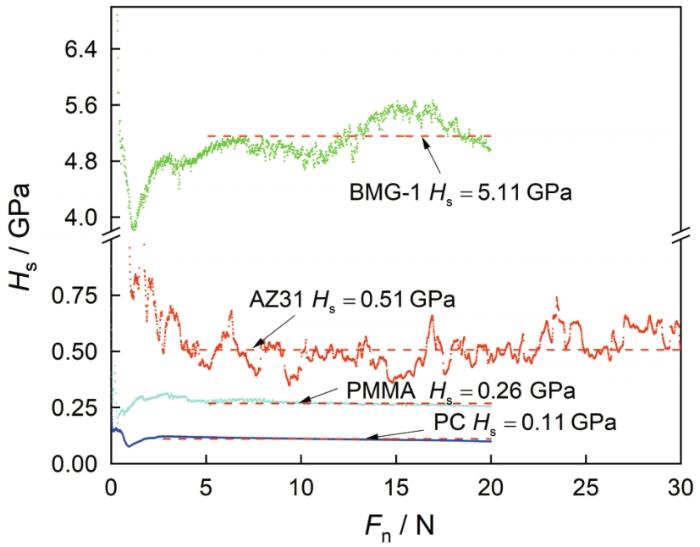
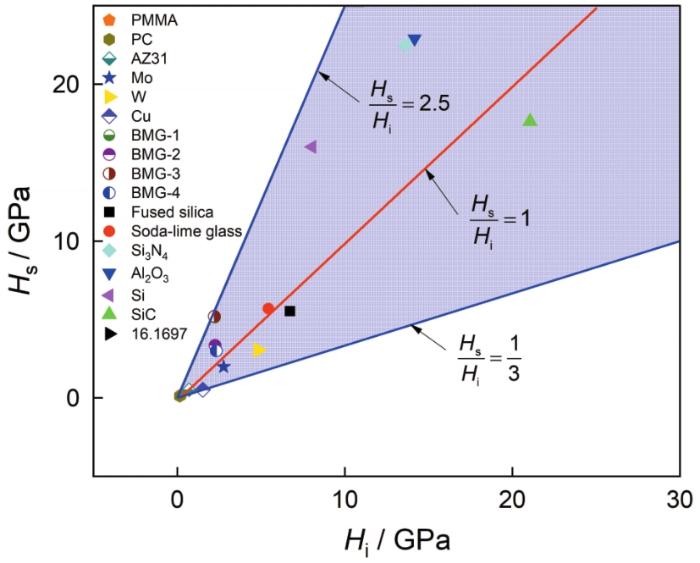
... 材料的划痕硬度与压痕硬度的关系,如图11所示.可以看出,划痕硬度随着压痕硬度的增大而增大,但是不同材料的划痕硬度与压痕硬度的比值不是一个恒定值,其比值范围为0.33~2.5[34,35].这一硬度比值与材料本身的弹性性能有关.同时,划痕硬度受压头形状影响较大.Briscoe等[38]发现,在不同锥角下对应的压痕硬度与划痕硬度的比值并不相同. ...
Scratch hardness of rare-earth substituted calcium aluminosilicate glasses
3
2019
... 划痕宽度可用来计算划痕硬度.划痕硬度可用于评估材料的耐磨性.与压痕硬度相比,划痕硬度更能反映划痕时一定体积材料产生塑性变形所需的功[34].在完全塑性材料的划痕过程中压头施加的法向载荷完全由压头前锥面下的材料承受,因此与压痕实验相比在同等载荷下压头会压入得更深,直至压头前锥面的接触面积达到相同的压痕接触面积.而对于纯弹性材料,由于划痕过程中压头后锥面材料瞬间恢复,压头施加的法向载荷由前后锥面共同承受,在压入深度方向材料产生与压痕实验相同的变形[8].大多数弹塑性材料的划痕变形行为处于这两者之间,这种划痕变形行为与材料的弹性恢复率[35]和实验采用的划痕速度[36]有关.材料的划痕硬度定义为[37] ...
... 材料的划痕硬度与压痕硬度的关系,如图11所示.可以看出,划痕硬度随着压痕硬度的增大而增大,但是不同材料的划痕硬度与压痕硬度的比值不是一个恒定值,其比值范围为0.33~2.5[34,35].这一硬度比值与材料本身的弹性性能有关.同时,划痕硬度受压头形状影响较大.Briscoe等[38]发现,在不同锥角下对应的压痕硬度与划痕硬度的比值并不相同. ...
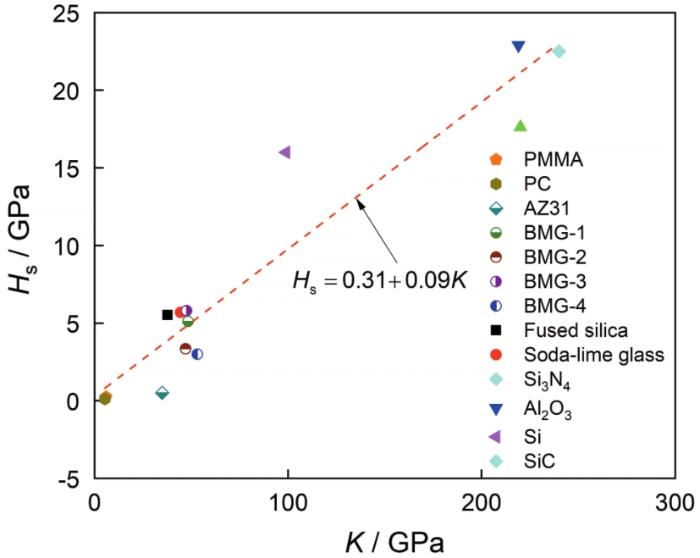
... 图12表明,划痕硬度与体积模量之间存在线性关系.实验结果与Sawamura等[39]观察到的结果一致.在划痕过程中,受材料堆积以及摩擦力的影响划痕消耗比压痕更多的能量用于材料变形,这种变形机制直接受材料的弹性性能影响.而弹性参数体积模量反映了材料键能密度分布的均匀性,这种均匀性与材料的划痕硬度密切相关[35]. ...
Strain-rate sensitivity of scratch hardness and deformation mechanism in nanocrystalline Ni under micro-scratch testing
1
2016
... 划痕宽度可用来计算划痕硬度.划痕硬度可用于评估材料的耐磨性.与压痕硬度相比,划痕硬度更能反映划痕时一定体积材料产生塑性变形所需的功[34].在完全塑性材料的划痕过程中压头施加的法向载荷完全由压头前锥面下的材料承受,因此与压痕实验相比在同等载荷下压头会压入得更深,直至压头前锥面的接触面积达到相同的压痕接触面积.而对于纯弹性材料,由于划痕过程中压头后锥面材料瞬间恢复,压头施加的法向载荷由前后锥面共同承受,在压入深度方向材料产生与压痕实验相同的变形[8].大多数弹塑性材料的划痕变形行为处于这两者之间,这种划痕变形行为与材料的弹性恢复率[35]和实验采用的划痕速度[36]有关.材料的划痕硬度定义为[37] ...
Effects of normal load on single-pass scratching of polymer surfaces
1
2006
... 划痕宽度可用来计算划痕硬度.划痕硬度可用于评估材料的耐磨性.与压痕硬度相比,划痕硬度更能反映划痕时一定体积材料产生塑性变形所需的功[34].在完全塑性材料的划痕过程中压头施加的法向载荷完全由压头前锥面下的材料承受,因此与压痕实验相比在同等载荷下压头会压入得更深,直至压头前锥面的接触面积达到相同的压痕接触面积.而对于纯弹性材料,由于划痕过程中压头后锥面材料瞬间恢复,压头施加的法向载荷由前后锥面共同承受,在压入深度方向材料产生与压痕实验相同的变形[8].大多数弹塑性材料的划痕变形行为处于这两者之间,这种划痕变形行为与材料的弹性恢复率[35]和实验采用的划痕速度[36]有关.材料的划痕硬度定义为[37] ...
The hardnesses of poly(methylmethacrylate)
1
1996
... 材料的划痕硬度与压痕硬度的关系,如图11所示.可以看出,划痕硬度随着压痕硬度的增大而增大,但是不同材料的划痕硬度与压痕硬度的比值不是一个恒定值,其比值范围为0.33~2.5[34,35].这一硬度比值与材料本身的弹性性能有关.同时,划痕硬度受压头形状影响较大.Briscoe等[38]发现,在不同锥角下对应的压痕硬度与划痕硬度的比值并不相同. ...
Scratch‐induced yielding and ductile fracture in silicate glasses probed by nanoindentation
3
2019
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
39]
5.44 | 0.2[50] | | Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... 图12表明,划痕硬度与体积模量之间存在线性关系.实验结果与Sawamura等[39]观察到的结果一致.在划痕过程中,受材料堆积以及摩擦力的影响划痕消耗比压痕更多的能量用于材料变形,这种变形机制直接受材料的弹性性能影响.而弹性参数体积模量反映了材料键能密度分布的均匀性,这种均匀性与材料的划痕硬度密切相关[35]. ...
评价多孔Si3N4陶瓷断裂韧性的新方法——单向压缩试验
3
2017
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 基于LEFM模型的断裂韧性分析,如图13所示.材料在达到裂纹失稳时的实验数据才可用于LEFM模型,因此较大载荷下的曲线平稳段才真正反映断裂韧性值.图13a中Si3N4在断裂韧性曲线平稳段的平均值为1.37 MPa·m1/2,与前人所得断裂韧性1.26 MPa·m1/2基本一致[40].图13b中PC在断裂韧性曲线平稳段的平均值为2.1 MPa·m1/2,与前人[17]所得断裂韧性2.2 MPa·m1/2一致.基于LEFM模型得到的所有材料的断裂韧性值Kc,列于表3.表3还列出了前人用传统方法(三点弯曲、紧凑拉伸和压痕法)得到的断裂韧性值.从表3可见,(紫铜和BMG-3),LEFM模型均能准确表征玻璃、陶瓷、聚合物和部分金属和金属玻璃材料的断裂韧性,得到的值与传统方法一致. ...
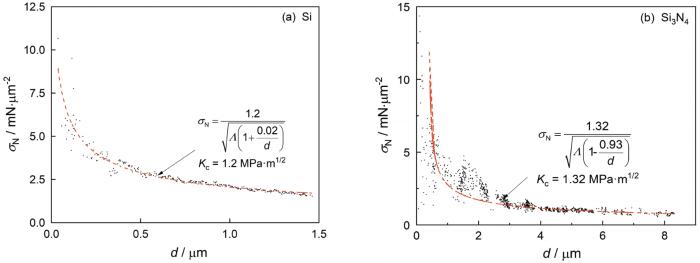
... 图15给出了用Hubler’s MESEL模型对(a) Si和(b) Si3N4的断裂韧性分析.利用此模型拟合数据得到Si和Si3N4的断裂韧性分别为1.2 MPa·m1/2和1.32 MPa·m1/2,与传统方法所得断裂韧性1.28 MPa·m1/2 [42]和1.26 MPa·m1/2 [40]基本一致.使用Hubler’s MESEL、Akono’s MESEL和LEFM模型计算出的断裂韧性值基本相同,但是都不能很好地表征大部分断裂韧性较大(>9 MPa·m1/2)的材料.这表明,在最大载荷在小于30 N的实验条件下这三个模型只适用于断裂韧性较小(<9 MPa·m1/2)的材料. ...
评价多孔Si3N4陶瓷断裂韧性的新方法——单向压缩试验
3
2017
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 基于LEFM模型的断裂韧性分析,如图13所示.材料在达到裂纹失稳时的实验数据才可用于LEFM模型,因此较大载荷下的曲线平稳段才真正反映断裂韧性值.图13a中Si3N4在断裂韧性曲线平稳段的平均值为1.37 MPa·m1/2,与前人所得断裂韧性1.26 MPa·m1/2基本一致[40].图13b中PC在断裂韧性曲线平稳段的平均值为2.1 MPa·m1/2,与前人[17]所得断裂韧性2.2 MPa·m1/2一致.基于LEFM模型得到的所有材料的断裂韧性值Kc,列于表3.表3还列出了前人用传统方法(三点弯曲、紧凑拉伸和压痕法)得到的断裂韧性值.从表3可见,(紫铜和BMG-3),LEFM模型均能准确表征玻璃、陶瓷、聚合物和部分金属和金属玻璃材料的断裂韧性,得到的值与传统方法一致. ...
... 图15给出了用Hubler’s MESEL模型对(a) Si和(b) Si3N4的断裂韧性分析.利用此模型拟合数据得到Si和Si3N4的断裂韧性分别为1.2 MPa·m1/2和1.32 MPa·m1/2,与传统方法所得断裂韧性1.28 MPa·m1/2 [42]和1.26 MPa·m1/2 [40]基本一致.使用Hubler’s MESEL、Akono’s MESEL和LEFM模型计算出的断裂韧性值基本相同,但是都不能很好地表征大部分断裂韧性较大(>9 MPa·m1/2)的材料.这表明,在最大载荷在小于30 N的实验条件下这三个模型只适用于断裂韧性较小(<9 MPa·m1/2)的材料. ...
单晶与多晶氧化铝陶瓷材料断裂性能与陶瓷基复合材料
2
1993
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 图14给出了用Akono’s MESEL模型对Fused silica和Al2O3的断裂韧性分析结果.此模型能很好拟合实验数据(相关系数大于0.9),得到的Fused silica和Al2O3的断裂韧性分别为0.76 MPa·m1/2和2.59 MPa·m1/2,与前人所得结果0.8 MPa·m1/2 [17]和2.346 MPa·m1/2 [41]相当接近.这表明,Akono’s MESEL模型能很好地表征材料的断裂韧性.根据Akono’s MESEL模型所得断裂韧性值与根据LEFM模型所得结果基本一致,但是不能准确表征大部分断裂韧性较大的材料(例如AZ31、钼、钨和部分非晶合金). ...
单晶与多晶氧化铝陶瓷材料断裂性能与陶瓷基复合材料
2
1993
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 图14给出了用Akono’s MESEL模型对Fused silica和Al2O3的断裂韧性分析结果.此模型能很好拟合实验数据(相关系数大于0.9),得到的Fused silica和Al2O3的断裂韧性分别为0.76 MPa·m1/2和2.59 MPa·m1/2,与前人所得结果0.8 MPa·m1/2 [17]和2.346 MPa·m1/2 [41]相当接近.这表明,Akono’s MESEL模型能很好地表征材料的断裂韧性.根据Akono’s MESEL模型所得断裂韧性值与根据LEFM模型所得结果基本一致,但是不能准确表征大部分断裂韧性较大的材料(例如AZ31、钼、钨和部分非晶合金). ...
Effect of temperature on fracture toughness in a single-crystal-silicon film and transition in its fracture mode
2
2008
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 图15给出了用Hubler’s MESEL模型对(a) Si和(b) Si3N4的断裂韧性分析.利用此模型拟合数据得到Si和Si3N4的断裂韧性分别为1.2 MPa·m1/2和1.32 MPa·m1/2,与传统方法所得断裂韧性1.28 MPa·m1/2 [42]和1.26 MPa·m1/2 [40]基本一致.使用Hubler’s MESEL、Akono’s MESEL和LEFM模型计算出的断裂韧性值基本相同,但是都不能很好地表征大部分断裂韧性较大(>9 MPa·m1/2)的材料.这表明,在最大载荷在小于30 N的实验条件下这三个模型只适用于断裂韧性较小(<9 MPa·m1/2)的材料. ...
Mg-based bulk metallic glasses: elastic properties and their correlations with toughness and glass transition temperature
13
2011
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
43]
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
43]
2.26 | 0.314[43] | | BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
43]
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
43]
2.22 | 0.317[43] | | BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
43]
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
43]
2.33 | 0.328[43] | Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
43]
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... [
43]
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... [
43]
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... [
43]
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
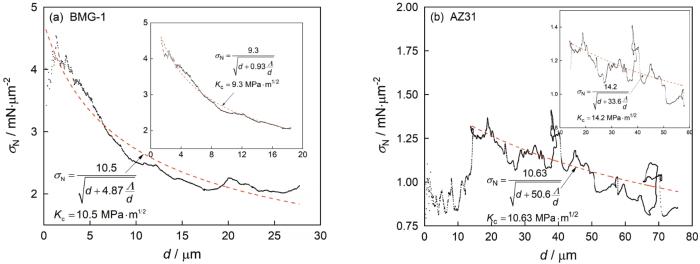
... 图16给出了用Liu’s MESEL模型对非晶合金BMG-1和AZ331的断裂韧性分析.用此模型拟合曲线得到BMG-1和AZ31的断裂韧性值分别为10.2 MPa·m1/2和10.63 MPa·m1/2,与前人所得结果8.2 MPa·m1/2 [43]和15.9 MPa·m1/2 [44]相差较大.用MESEL模型拟合曲线时,选择的拟合曲线段对结果有较大的影响.选择曲线较为平滑的中间段进行拟合(见插图),得到BMG-1和AZ331的断裂韧性分别为9.3 MPa·m1/2和14.2 BMG-1和AZ331,与前人所得结果基本一致.这表明,在用MESEL模型拟合曲线以得到断裂韧性时,应当选择合适的拟合区间(一般为曲线的中间段).与其他三种模型比较,Liu’s MESEL模型能较为准确地表征大部分断裂韧性较大的金属和非晶合金材料.这表明,四种模型都有一定的材料适用范围. ...
Effect of texture on fracture toughness in extruded AZ31 magnesium alloy
2
2005
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
... 图16给出了用Liu’s MESEL模型对非晶合金BMG-1和AZ331的断裂韧性分析.用此模型拟合曲线得到BMG-1和AZ31的断裂韧性值分别为10.2 MPa·m1/2和10.63 MPa·m1/2,与前人所得结果8.2 MPa·m1/2 [43]和15.9 MPa·m1/2 [44]相差较大.用MESEL模型拟合曲线时,选择的拟合曲线段对结果有较大的影响.选择曲线较为平滑的中间段进行拟合(见插图),得到BMG-1和AZ331的断裂韧性分别为9.3 MPa·m1/2和14.2 BMG-1和AZ331,与前人所得结果基本一致.这表明,在用MESEL模型拟合曲线以得到断裂韧性时,应当选择合适的拟合区间(一般为曲线的中间段).与其他三种模型比较,Liu’s MESEL模型能较为准确地表征大部分断裂韧性较大的金属和非晶合金材料.这表明,四种模型都有一定的材料适用范围. ...
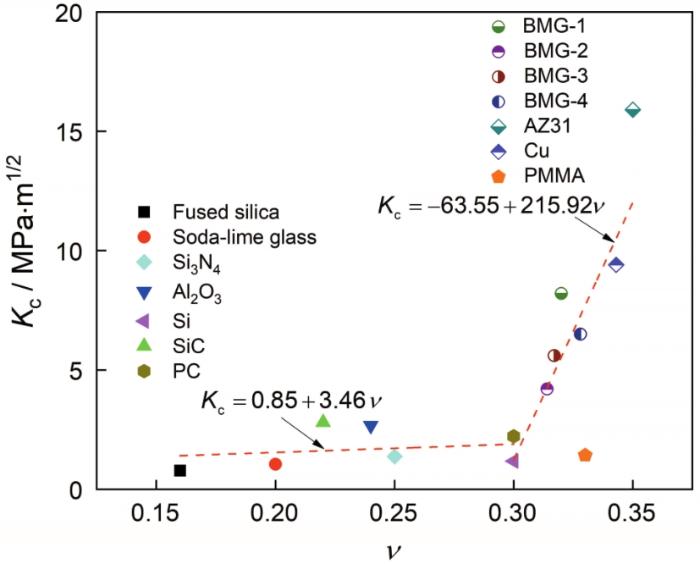
Critical Poisson's ratio between toughness and brittleness
1
2016
... 图17给出了9种材料的断裂韧性Kc与泊松比v的关系.可以看出,断裂韧性随泊松比的增大而增大.其原因是,断裂韧性是材料塑性流动与断裂相互竞争的结果,因此与材料的弹性性能有关.而泊松比在一定程度上反映了材料的弹性性能.泊松比的减小增加了主应力空间中拉应力状态和压应力状态之间断裂轨迹的不对称性[45],因此高泊松比材料具有更好的抵抗裂纹扩展能力. ...
Pressure dependence of the elastic constants of poly(methyl methacrylate)
2
1995
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
... [
46]
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
The elastic behaviour of polycarbonate in the glassy state determined by Brillouin scattering
1
1995
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Nanoindentation characteristics on polycarbonate polymer film
1
2004
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Surface effects on Young's modulus and hardness of fused silica by nanoindentation study
1
2007
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
钢化对钠钙硅玻璃弹性性能的影响
1
2009
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
钢化对钠钙硅玻璃弹性性能的影响
1
2009
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Pseudo-potential calculations of structural, elastic and thermal properties of Si3N4
1
2011
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Microstructure and mechanical properties of TiAlN/Si3N4 nano-multilayers synthesized by reactive magnetron sputtering
1
2009
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Theoretical structure determination of γ-Al2O3
1
2001
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
On the reliability of nanoindentation hardness of Al2O3 films grown on Si-wafer by atomic layer deposition
1
2014
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
1
2001
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Nanoindentation on single-crystal Si modified by 100 keV Cr+ implantation
1
2008
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Theoretical study of thermodynamics properties and bulk modulus of SiC under high pressure and temperature
1
2014
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Fracture toughness determinations by indentation
1
1976
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
Elasticity and internal friction of magnesium alloys at room and elevated temperatures
1
2018
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
AZ31镁合金热轧开坯变形行为的有限元模拟
1
2009
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
AZ31镁合金热轧开坯变形行为的有限元模拟
1
2009
... The friction coefficient and elastic-plastic properties of the materials
Table 2| Materials | μ0 | μavg | μcal | Hs/GPa | K/GPa | Hi/GPa | v |
|---|
| PMMA | 0.09 | 0.39 | 0.52 | 0.26 | 5.93[46] | 0.26 | 0.33[46] |
| PC | 0.16 | 0.63 | 0.63 | 0.11 | 5.3[47] | 0.14 | 0.3[48] |
| Fused silica | 0.048 | 0.06 | 0.08 | 5.53 | 37.7[39] | 6.73 | 0.16[49] |
| S-L glass | 0.057 | 0.08 | 0.09 | 6.19 | 44.4[39] | 5.44 | 0.2[50] |
| Si3N4 | 0.042 | 0.058 | 0.07 | 22.5 | 239.9[51] | 13.6 | 0.25[52] |
| Al2O3 | 0.045 | 0.075 | 0.07 | 22.9 | 219[53] | 14.16 | 0.24[54] |
| Si | 0.035 | 0.037 | 0.04 | 16 | 99[55] | 8.05 | 0.3[56] |
| SiC | 0.045 | 0.08 | 0.07 | 1.78 | 220[57] | 21.05 | 0.22[58] |
| AZ31 | 0.18 | 0.54 | 0.66 | 0.51 | 34.9[59] | 0.7 | 0.35[60] |
| Mo | 0.045 | 0.44 | 0.45 | 1.98 | NA | 2.77 | NA |
| W | 0.04 | 0.45 | 0.44 | 3.06 | NA | 4.83 | NA |
| Cu | 0.2 | 0.78 | 0.69 | 0.52 | NA | 1.52 | 0.343 |
| BMG-1 | 0.09 | 0.26 | 0.52 | 5.11 | 48.3[43] | 2.25 | 0.32[43] |
| BMG-2 | 0.12 | 0.43 | 0.57 | 5.2 | 47[43] | 2.26 | 0.314[43] |
| BMG-3 | 0.124 | 0.35 | 0.57 | 3.35 | 47.6[43] | 2.22 | 0.317[43] |
| BMG-4 | 0.16 | 0.328 | 0.63 | 3 | 53.1[43] | 2.33 | 0.328[43] |
Note:μ0—Initial friction coefficient, μavg—Average friction coefficient, μcal—Calculated friction coefficient, Hs—Scratch hardness, K—Bulk modulus, Hi—Indentation hardness, v—Poisson's ratio ...
The mechanical properties of PMMA and its copolymers with ethyl methacrylate and butyl methacrylate
1
1994
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
Statistical analysis of fracture toughness of soda-lime glass determined by indentation
1
2001
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
Ballistic performance of armour ceramics: Influence of design and structure. Part 1
1
2010
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
Enhanced fracture toughness and strength in bulk nanocrystalline Cu with nanoscale twin bundles
1
2009
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
The influence of silicon on the strength and fracture toughness of molybdenum
1
2007
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...
Effect of rhenium addition on fracture toughness of tungsten at elevated temperatures
1
1995
... Fracture toughness calculated by different formulas (MPa·m
1/2)
Table 3| Materials | Eq.(7) | Eq.(10) | Eq.(12) | Eq.(13) | SENB/CNB/IF method |
|---|
| PMMA | 1.42 | 1.39 | 1.07 | 2.16 | 1.5[61] |
| PC | 2.1 | 2.87 | 2.7 | 6.6 | 2.2[17] |
| Fused silica | 0.78 | 0.76 | 0.73 | 1.26 | 0.8[17] |
| S-L glass | 1.05 | 1.09 | 1.09 | 1.9 | 0.75[62] |
| Si3N4 | 1.37 | 1.32 | 1.32 | 2.3 | 1.26[40] |
| Al2O3 | 2.67 | 2.59 | 2.59 | 5.66 | 2.346[41] |
| Si | 1.18 | 1.2 | 1.2 | 2.08 | 1.28[42] |
| SiC | 2.86 | 2.91 | 2.92 | 6.2 | 2.8[63] |
| Cu | 8.6 | 8.32 | 8.29 | 15.24 | 9.4[64] |
| BMG-3 | 5 | 3.45 | 3.05 | 5.33 | 5.6[43] |
| BMG-2 | 7 | 4 | 4.11 | 7.3 | 4.2[43] |
| BMG-4 | 8.6 | 6.8 | 6.68 | 11.97 | 6.5[43] |
| Mo | 11 | 8 | 12.3 | 24.1 | 24.2[65] |
| W | 10.21 | 5.75 | 5.9 | 12.88 | 14[66] |
| AZ31 | 3.79 | 5 | 4.82 | 14 | 15.9[44] |
| BMG-1 | 5.64 | 5.64 | 5.62 | 9.3 | 8.2[43] |
Note: The bold font indicates that the calculated fracture toughness value is consistent with that obtained by the traditional method ...