Dynamic Recrystallization of Ti-6Al-4V Alloy During Hot Compression

doi:10.11901/1005.3093.2020.569

Ti-6Al-4V合金热压缩过程中的动态再结晶

刘超¹, 王鑫¹, 门月¹, 张浩�?/span>¹, 张思�?/span>¹, 周舸^,¹, 陈立�?/span>¹, 刘海�?/span>²

1.沈阳工业大学材料科学与工程学�?沈阳 110870

2.上海航天精密机械研究所上海 201600

Dynamic Recrystallization of Ti-6Al-4V Alloy During Hot Compression

LIU Chao¹, WANG Xin¹, MEN Yue¹, ZHANG Haoyu¹, ZHANG Siqian¹, ZHOU Ge^,¹, CHEN Lijia¹, LIU Haijian²

1.School of Materials Science and Engineering, Shenyang University of Technology, Shenyang 110870, China

2.Shanghai Spaceflight Precision Machinery Institute, Shanghai 201600, China

通讯作�? 周舸，副教授�?a href=\"mailto:zhouge@sut.edu.cn\">zhouge@sut.edu.cn，研究方向为钛合金、高温合金热变形行为及变形机�?/span>

收稿日期: 2020-12-28 修回日期: 2021-04-22 网络出版日期: 2021-09-07

基金资助:

国家自然科学基金. 51805335

Corresponding authors: ZHOU Ge, Tel: 18602408585, E-mail:zhouge@sut.edu.cn

Received: 2020-12-28 Revised: 2021-04-22 Online: 2021-09-07

作者简�?About authors

刘超，男�?994年生，硕�?

摘要

在变形温度为870~960℃、应变速率�?×10^-4 s^-1~5×10^-2 s^-1的条件下对Ti-6Al-4V合金进行单道次等温压缩实验，测出其应�?应变曲线并建立KM模型、Poliak-Jonas模型和Avrami模型，较为系统地描述了这种合金动态再结晶过程中的流变应力、临界应变量、组织演变动力学等的特征。将动态再结晶组织的转变体积分数引入Prasad功率耗散率模型，得到了Ti-6Al-4V合金动态再结晶过程中能量的变化规律并结合微观组织表征揭示了这种合金的动态再结晶机理。结果表明：随着变形温度的提高和应变速率的降低，Ti-6Al-4V合金的动态再结晶临界应变量减小，组织转变的体积分数增大。发生完全动态再结晶时的功率耗散率大�?.34，形核机制为位错诱导的弓出形核机制�?/span>

关键词： 金属材料 ; Ti-6Al-4V合金 ; 动态再结晶 ; 物理模型 ; 热压缩变�?/kwd> ; 微观组织

Abstract

The stress-strain curves of Ti-6Al-4V alloy during hot deformation by applied strain rate within the range of 5×10^-4~5×10^-2 s^-1 at 870~960°C were measured via single-pass isothermal compression test. The dynamics characteristics of rheological stress, critical strain capacity and structure evolution of the alloy during dynamic recrystallization were systematically illustrated by means of KM model, Poliak-Jonas model, and Avrami model. Then a concept of volume fraction of the microstructure transformation, i.e., the portion of the alloy that has been underwent microstructure transformation during dynamic recrystallization, was introduced into the so called prasad power dissipation rate model, thus the energy variation of the alloy during dynamic recrystallization was acquired. Further, taking both of the acquired energy variation and the observed microstructure evolution characteristics together into consideration, the dynamic recrystallization mechanism of Ti-6Al-4V alloy may be revealed. It follows that the critical strain capacity of Ti-6Al-4V during dynamic recrystallization decreased and the structural transformation volume fraction increased following the rise of deformation temperature or the decline of strain rate. The power dissipation rate upon complete dynamic recrystallization is larger than 0.34, and the forming mechanism is a dislocation-induced arcuation nucleation mechanism.

Keywords�?/strong> metallic materials ; Ti-6Al-4V ; dynamic recrystallization ; physical models ; hot compression deformation ; microstructure

PDF (12830KB) 元数�?/a> 多维度评�?/a> 相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘超, 王鑫, 门月, 张浩�? 张思�? 周舸, 陈立�? 刘海�? Ti-6Al-4V合金热压缩过程中的动态再结晶. 材料研究学报[J], 2021, 35(8): 583-590 DOI:10.11901/1005.3093.2020.569

LIU Chao, WANG Xin, MEN Yue, ZHANG Haoyu, ZHANG Siqian, ZHOU Ge, CHEN Lijia, LIU Haijian. Dynamic Recrystallization of Ti-6Al-4V Alloy During Hot Compression. Chinese Journal of Materials Research[J], 2021, 35(8): 583-590 DOI:10.11901/1005.3093.2020.569

Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4]。近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂。因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点。杨博文^[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确性。张治民^[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据。Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础。上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关键。发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机制。因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一。为此，张君�?sup>[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关系。本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规律。最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为�?/p>

1 实验方法

实验用材料为铸造态Ti-6Al-4V合金，其成分(质量分数�?)为：Al 6.2，V 4.1，Fe�?.3，C�?.1，Ti余量�?/p>

将该合金加工成直径为10 mm长度�?5 mm的热压缩试样，将两端面加工成深度�?.2 mm的凹槽。使用Gleeble-3800�?力模拟实验机进行单道次等温压缩实验，参数为：温度�?70~960℃，间隔30℃，应变速率�?×10^-4 s^-1~5×10^-2 s^-1，工程应变：0.3�?.4�?.6。实验后水冷，以保留完整的高温组织�?/p>

用型号为OLYMPUS GX51光学电子显微镜下进行金相观察，腐蚀的第一阶段(晶界腐蚀)：浸蚀剂为6 mL HNO₃+100 mL H₂O+3 mL HF；第二阶�?区分β�?�?8 mL C₂H₂O₄·2H₂O(20mass%)�? g Fe(NO₃)₃�? mL HF。用型号为Tecnai G² 20透射电镜观察微观组织，试样的制备：酸喷试剂为，甲醇∶正丁醇∶高氯�?60%�?4%�?%。电流值：40~45 mA，电压值：50 V，温度：-40�?35℃之间�?/p>

2 实验结果

2.1 Ti-6Al-4V合金的热变形本构关系

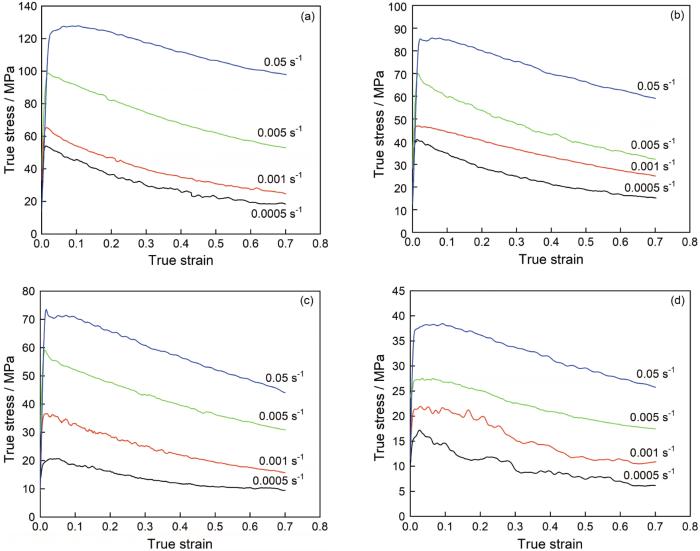
�?给出了Ti-6Al-4V合金应力-应变曲线。从�?可见，该合金热变形流变应力随着变形温度的提高而降低，随着应变速率的提高而增大。同时，在应变初始阶段流变应力迅速增大，达到峰值后降低。应变速率�?.005 s^-1时，流变应力随着变形量的增大(ε�?.5)逐渐趋于稳定状态。应变速率�?.005 s^-1时流变应力随着变形量的增大而减小，此时动态软化机制起主导作用�?/p>

�?

新窗口打开| 下载原图ZIP| 生成PPT

�?   Ti-6Al-4V合金在不同温度变形的真应�?应变曲线

Fig.1   True stress-true strain curves of Ti-6Al-4V alloy (a) 870�? (b) 900�? (c) 930�? (d) 960�?/strong>

从能量角度分析，该合金的热变形过程是一个热激活过程，流变应力与变形工艺参数间满足Arrhenius本构关系模型^[15]

$ε^{n_{3}} \dot{ε} e x p (\frac{Q}{R T}) = A_{1} σ^{n_{1}}$ (1)

其中n₃为与应变有关的参数。经过数学运算可�?/p>

$l n σ = B_{0} + B_{1} l n \dot{ε} + B_{2} \frac{1}{T} + B_{3} l n ε$ (2)

根据�?中的实验数据分别分析Ti-6Al-4V合金热变形过程中的ln $σ$ -ln $\dot{ε}$ 、ln $σ$ -ln $ε$ 、ln $σ$ -1/ $T$ ，可得ln $σ$ -1/ $T$ 之间的近似线性关系，而ln $σ$ -ln $\dot{ε}$ 、lnσ-lnε之间均服从近抛物线关系。为了更好的描述热变形过程中的本构关系，引入应变速率与温度项修正因子lnέ/T，可得到该合金热变形过程的本构方�?/p>

$l n σ = b_{0} + b_{1} l n ε + b_{2} {(l n ε)}^{2} + b_{3} {(l n ε)}^{3} + b_{4} l n \dot{ε} + b_{5} {(l n \dot{ε})}^{2} + b_{6} {(l n \dot{ε})}^{3} + b_{7} \frac{1}{T} + b_{8} \frac{l n \dot{ε}}{T}$ (3)

用多元线性回归法并结�?a class="table-icon" style="color:#2150f9" href="#F1"; id="inline_content�?">�?的实验数据，可计算出公式(3)中的各个参数，其值列�?a class="table-icon" style="color:#2150f9" href="#T1"; id="inline_content�?">�?�?/p>

Table 1

�?

�?   Ti-6Al-4V合金本构关系模型的参�?/span>

Table 1  Parameters in constitutive equation of Ti-6Al-4V alloy

Parameters Value Parameters Value
b₀ -12.9616 b₅ 0.48118
b₁ -0.5318 b₆ 0.03365
b₂ -0.05727 b₇ 23.7294
b₃ 0.0309 b₈ 1.02584
b₄ 0.81679

新窗口打开| 下载CSV

热变形本构关系模型，反映了Ti-6Al-4V合金热变形过程中流变应力(σ)与应变速率( $\dot{ε}$ )、变形温�?t)、变形量(ε)之间的多元线性关系。使用该模型，可定量计算出不同热变形工艺下的流变应力值。该应力值，是加工硬化与软化共同作用的结果。但是就单一软化过程而言，使用模型不能进行定量分析。该合金软化效应的本质是动态再结晶，因此需要研究其热变形过程的动态再结晶�?/p>

2.2 Ti-6Al-4V合金动态再结晶的物理模�?

动态再结晶是金属材料热变形时的一种重要的软化机制，其本质可用动态再结晶临界应变模型和动态再结晶动力学模型描述�?/p>

Poliak和Jonas^[16]认为，发生动态再结晶时应变与应力之间的关系为

$\frac{- {�?/mo>}^{2} θ}{�?/mo>σ} = 0$ (4)

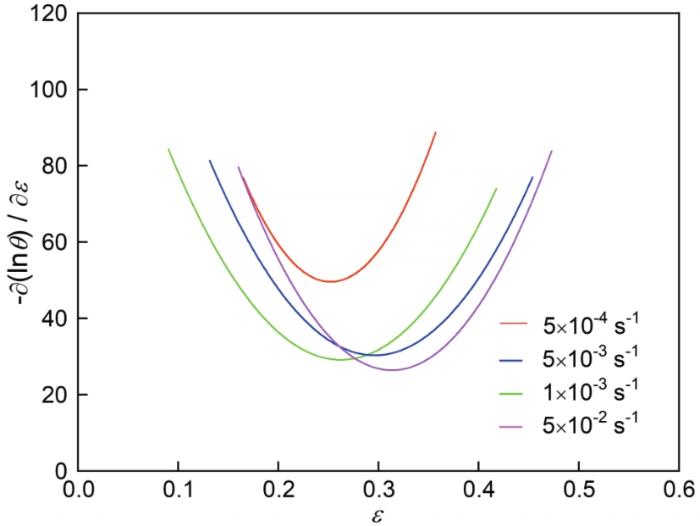
其中θ=dσ/dε为加工硬化率�?i>σ为流变应力。根�?.1节中σ-ε的本构关系，Ti-6Al-4V合金在热变形过程中发生动态再结晶时的临界应变模型�?/p>

$\frac{- �?/mo>(l n θ)}{�?/mo>ε} = B_{0} + B_{1} ε + B_{2} ε^{2}$ (5)

�?给出了该合金�?30℃不同应变速率下的 $\frac{- �?/mo>(l n θ)}{�?/mo>ε} - ε$ 关系曲线。从�?可见�?span class="formulaText"> $\frac{- �?/mo>(l n θ)}{�?/mo>ε}$ =0对应的应变量即为临界应变�?i>ε_c。可计算出Ti-6Al-4V合金在不同变形条件下�?i>ε_c，如�?所示�?/p>

�?

新窗口打开| 下载原图ZIP| 生成PPT

�?   Ti-6Al-4V合金不同应变速率�?i>-􀆟(lnθ)/􀆟ε�?i>ε的关�?/strong>

Fig.2   􀆟(lnθ)/􀆟ε-ε curves of Ti-6Al-4V alloy at different strain rates

Table 2

�?

�?   Ti-6Al-4V合金动态再结晶临界应变�?ε_c)

Table 2  Critical strain during high deformation of Ti-6Al-4V alloy

Strain rate/s^-1 ε_c
870�?/th> 900�?/th> 930�?/th> 960�?/th>
5×10^-4 0.3089 0.2936 0.2724 0.2536
1×10^-3 0.3177 0.2991 0.2872 0.2701
5×10^-3 0.3302 0.3156 0.3007 0.2841
5×10^-2 0.3498 0.3301 0.3191 0.2951

新窗口打开| 下载CSV

根据Poliak-Jonas临界应变模型，使�?a class="table-icon" style="color:#2150f9" href="#T2"; id="inline_content�?">�?中的数据对其热变形过程中热力学不可逆条件下的临界应�?i>ε_c进行多元线性回归，可得Ti-6Al-4V合金的动态再结晶临界应变模型

$ε_{c} = e x p (- 2.739 + 0.029 l n \dot{ε} + \frac{1554.09}{t})$ (6)

�?给出了Ti-6Al-4V合金870~960℃、应变速率�?×10^-4~5×10^-2 s^-1条件下热压缩过程中动态再结晶临界应变量的分布规律。从�?可以看出，在高温、低应变速率条件下该合金的动态再结晶临界应变�?i>ε_c较小，因此动态再结晶容易发生。而随着变形温度的降低和应变速率的提高临界应变量逐渐增大，动态再结晶出现了一定的滞后。临界应变模型描述了合金在热变形过程中发生动态再结晶的临界状态，但是不能描述动态再结晶组织的演化和能量耗散。因此，需要从动力学角度进行分析�?/p>

�?

新窗口打开| 下载原图ZIP| 生成PPT

�?   Ti-6Al-4V合金的动态再结晶临界应变量关�?/strong>

Fig.3   Relation of critical strain of Ti-6Al-4V alloy for dynamic recrystallization

Avrami提出了金属材料动态再结晶过程中动力学转变经典模型^[17]

$X_{d} = 1 - e x p \{- k {[\frac{ε - ε_{c}}{ε_{p}}]}^{n}\}$ (7)

其中ε为应变值；ε_c为临界应变量�?i>ε_p为峰值应力应变量；K₁，K₂为常数；X_d为动态再结晶分数。据文献[18]�?i>ε_c< ε_p< ε_s�?i>X_d与流变应力之间的关系�?/p>

$X_{d} = \frac{(σ_{c} - σ)}{({σ_{s s}}^{A} - {σ_{s s}}^{B})}$ (8)

其中 $σ_{c}$ 为临界应力， $σ$ 为流变应力， $σ_{s s}^{B}$ 为稳态应力， $σ_{s s}^{A}$ 为未发生动态再结晶时的稳态应力。求解该合金的动力学模型时，选取本文的热压缩实验为作为基础数据�?i>ε_c�?a class="table-icon" style="color:#2150f9" href="#T2"; id="inline_content�?">�?可得�?i>ε_p�?i>ε_s�?span class="formulaText"> $σ_{s s}^{B}$ �?span class="formulaText"> $σ_{s s}^{A}$ �?i>σ_c�?i>σ值可在应�?应变曲线(�?)上读取。用多项式拟合方法求�?xref ref-type="disp-formula" rid="DF7">公式(7)�?8)，分别得到n=1.37，k=0.72，因此Ti-6Al-4V合金动力学方程为

$X_{d} = 1 - e x p \{- 0.72 {[\frac{ε - ε_{c}}{ε_{p}}]}^{1.37}\}$ (9)

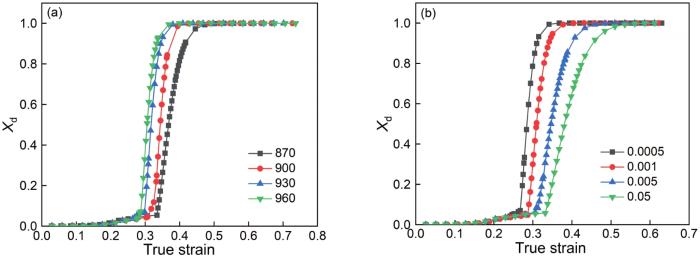
�?给出了Ti-6Al-4V合金�?30℃不同应变速率(5×10^-4~5×10^-2 s^-1)下热变形过程中的动态再结晶体积分数的演化规律，整体特征呈现“S”型变化趋势。应变量达到ε_c时该点曲线不再平滑而出现转折点，表示动态再结晶开始。当应变量大�?i>ε_c�?i>X_d迅速增大，并随着应变量的增大而逐渐趋于稳定，直�?i>X_d接近1，此时发生完全动态再结晶。对�?a class="table-icon" style="color:#2150f9" href="#F4"; id="inline_content�?">�?a、b可得，该合金�?30~960℃和0.001~0.005 s^-1条件下变形时发生完全动态再结晶时的应变量分别为0.341�?.352，在870~900℃和0.005~0.05 s^-1条件下变形时发生完全动态再结晶时的应变量出现滞后，应变量大�?.4。上述结果的本质，是该合金在再结晶组织转变时发生了能量变化�?/p>

�?

新窗口打开| 下载原图ZIP| 生成PPT

�?   Ti-6Al-4V合金在不同条件下动态再结晶体积分数X_d的演�?/strong>

Fig.4   Evolution of dynamic recrystallization volume fraction X_d in Ti-6Al-4V alloy under different conditions (a) strain rate 0.005 s^-1, (b) temperature 930�?/strong>

2.3 Ti-6Al-4V合金的动态再结晶能量耗散模型

从物理学角度，金属材料发生动态再结晶时伴随着能量的转�?P)，包括材料发生变形需要的能量(G)和组织演变消耗的能量(J)。发生动态再结晶组织转变势必引起原子势能的变化，而变形过程中位错运动、晶界滑移等则以热量形式耗散。因此，根据Prasad^[19]等人提出的耗散结构理论模型

$η = \frac{J}{J_{m a x}} = \frac{2 m}{m + 1}$ (10)

使用公式(8)�?i>X_d引入Prasad模型，可�?/p>

$\begin{array}{l} m = \frac{d J}{d G} - \frac{�?/mo>lnσ_{D R X}}{�?/mo>lnε} = \frac{\dot{ε}}{σ_{D R X}} \frac{d σ_{D R X}}{d X_{D R X}} \frac{d X_{D R X}}{d \dot{ε}} \\ = \frac{\dot{ε}}{σ_{D R X}} (σ_{s s}^{A} - σ_{s s}^{B}) \frac{d X_{D R X}}{d \dot{ε}} \end{array}$ (11)

求解公式(10)�?11)可得该合金应变为0.3�?.4时的动态再结晶功率耗散率等值曲线，�?a class="table-icon" style="color:#2150f9" href="#F5"; id="inline_content�?">�?所示�?/p>

�?

新窗口打开| 下载原图ZIP| 生成PPT

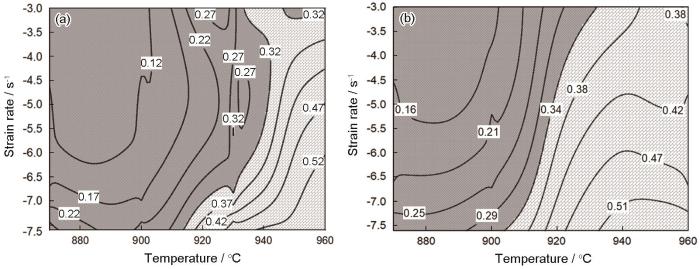
�?   Ti-6Al-4V合金动态再结晶功率耗散率的分布

Fig.5   Dynamic recrystallization power dissipation of Ti-6Al-4V alloy at different temperatures and strain rates (a) ε=0.3, (b) ε=0.4

Ti-6Al-4V合金在变形温度为930~960℃、应变速率�?×10^-4~10^-3 s^-1时，动态再结晶的临界应变量ε_c�?0.2536~0.2872)。变形量�?.3时开始发生动态再结晶，此�?i>X_d�?6.75%~10.98%)，说明该合金未发生完全动态再结晶，流变应力缓慢降�?�?)，合金的功率耗散�?i>η值大�?.3(�?a)。当变形量增大至0.4、温度大�?00℃和应变速率小于0.05 s^-1该合金发生完全动态再结晶�?i>X_d接近�?，此时功率耗散�?i>η值大�?.34(�?b)。而当温度低于900℃时�?i>X_d�?49.25%~77.38%)发生未完全动态再结晶，功率耗散�?i>η值为0.16~0.34(�?b)。因此，Ti-6Al-4V合金在上述热变形过程中发生完全动态再结晶的临界能量条件为η值大�?.34�?/p>

2.4 Ti-6Al-4V合金的动态再结晶显微组织

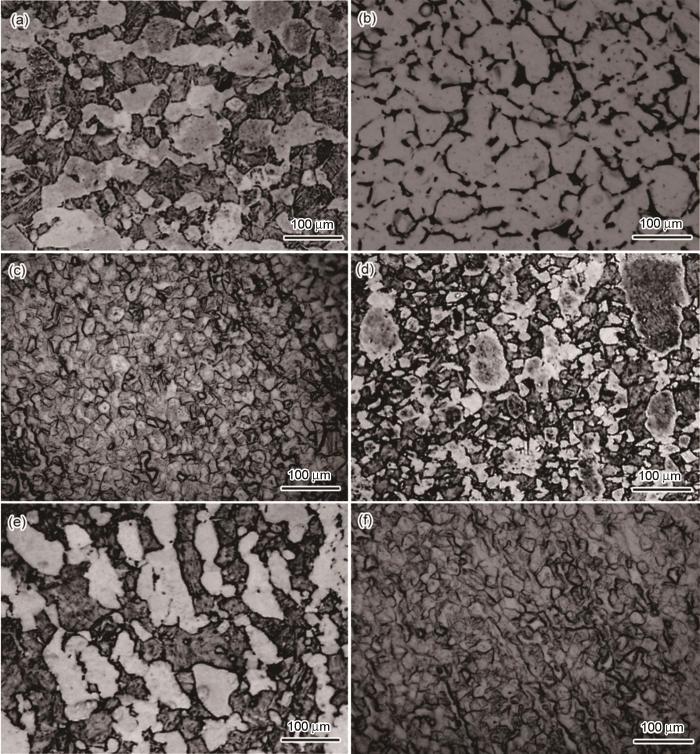
�?a~f给出了Ti-6Al-4V合金单道次热压缩变形前后的金相显微组织照片�?a class="table-icon" style="color:#2150f9" href="#F6"; id="inline_content�?">�?a给出了原始铸态组织，平均晶粒尺寸约为80 μm�?a class="table-icon" style="color:#2150f9" href="#F6"; id="inline_content�?">�?b~f给出了该合金在不同热变形条件下的组织，包括动态再结晶临界组织、不完全再结晶组织、完全再结晶组织。在变形�?i>ε�?.3�?i>T=930℃和έ=0.0005 s^-1条件下原始铸态晶粒周围出现再结晶晶粒，呈现细小、等轴化趋势，且晶界呈现锯齿�?�?b)，表明合金开始发生动态再结晶，此�?X_d=8.98%。在T=870℃和έ=0.05 s^-1条件下只有少部分组织发生了动态再结晶�?i>X_d�?%，其金相显微组织与原始铸态组织相�?�?e)。上述结果，验证了本文建立的动态再结晶动力学模型的可靠性。当变形量增大至0.4时该合金发生了完全动态再�?X_d=100%)，金相组织呈现大量细小的等轴状，原始铸态粗大晶粒消失，平均晶粒尺寸约为10 μm�?�?c)，功率耗散�?i>η=0.3~0.34，此时的组织热加工性能良好。随着温度的降�?930℃→870�?�?i>X_d�?49.25%~77.38%)，发生部分动态再结晶(�?d)。其原因是，该合金发生动态再结晶需要的驱动力随着变形温度的降低而降低，不能满足发生完全再结晶组织转变的能量要求，此时功率耗散�?i>η值为0.16~0.3。该合金�?i>T=960℃�?έ=0.005 s^-1�?i>ε=0.6条件下变形时发生完全动态再结晶，晶粒尺寸约�?1.3 μm�?i>X_d=100%�?i>η大于0.32。其原因是，随着变形量的增大变形储能增加，在较高温度下原子扩散能力增大和位错运动加剧，使动态再结晶形核率提高。同时，应变速率较低使形核的新晶粒有充分的时间合并和长大�?/p>

�?

新窗口打开| 下载原图ZIP| 生成PPT

�?   Ti-6Al-4V合金的金相照�?/strong>

Fig.6   Microstructures of Ti-6Al-4V alloy (a) initial; (b) T=930�? έ=0.0005 s^-1, ε=0.3; (c) T=930�? έ=0.0005 s^-1, ε=0.4; (d) T=870�? έ=0.0005 s^-1, ε=0.3; (e) T=870�? έ=0.05 s^-1, ε=0.3; (f) T=960�? έ=0.005 s^-1, ε=0.6

�?给出了Ti-6Al-4V合金发生动态再结晶过程的TEM明场像。在T=930℃发�?i>α�?i>β的相转变，会影响合金的动态再结晶。结�?a class="table-icon" style="color:#2150f9" href="#F1"; id="inline_content�?">�?c，在不同软化机制的作用下曲线达到稳态，此时动态再结晶的形核与长大速率趋近于平衡，体系内出现动态再结晶过程不同阶段的组织，因此需要观察和表征再结晶晶粒形核长大过程的微观组织。变形晶粒内的位错密度较低，亚晶粒尺寸较大，在三叉晶界附近出现位错富集且发生再结晶形核；再结晶晶界呈凹凸状且由低位错一侧向高位错一侧迁移，�?a class="table-icon" style="color:#2150f9" href="#F7"; id="inline_content�?">�?a所示。对�?a中的再结晶晶界处进行高倍数观察(�?b，可见原始晶界两侧产生大量的位错，位错滑移、攀移、交滑移逐渐形成稠密位错墙，且晶界向位错密度较大一侧凸出，晶界发生出明显的弯曲。随着变形的进行原始晶界出现起伏褶皱，晶内几乎没有晶界，大部分原始组织�?~3层再结晶晶粒取代，变形晶粒呈长条状，再结晶呈现前沿三叉晶界形核、孪晶界和亚晶界辅助形核效应。因此，该合金在低应变速率时动态再结晶在三叉晶界处形核，且晶界易于迁移，其形核机制为位错诱导的弓出形核�?/p>

�?

新窗口打开| 下载原图ZIP| 生成PPT

�?   Ti-6Al-4V合金的TEM照片

Fig.7   Microstructures of Ti-6Al-4V alloy (T=930�? έ=0.0005 s^-1, ε=0.3)

3 结论

(1) Ti-6Al-4V合金热变形过程中的峰值应力和稳态应力都随着应变速率的提高和温度的降低而增大，且表现出明显的应变速率敏感性�?/p>

(2) 使用本文建立的Ti-6Al-4V合金动态再结晶过程的Arrhenius本构模型、临界应变模型、动力学模型、功率耗散率模型得到了该合金发生动态再结晶时的临界应变�?i>ε_c�?0.2536~0.3498)，动态再结晶体积分数X_d随着应变速率的提高和温度的降低而减小，动力学曲线出现典型的“S”型特征，发生完全再结晶的功率耗散�?i>η值大�?.34，发生不完全再结晶的η值为0.16~0.34�?/p>

(3) 根据对Ti-6Al-4V合金的TEM表征和分析，其在热变形过程中动态再结晶的形核机制为位错诱导的弓出形核�?/p>

参考文�?

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]
Salishchev G A, Aliyev R M, Valiakhmetov O R.
Development of Ti-6Al-4V sheet with low temperature superplastic properties
[J]. J. Mater. Process. Tech., 2001, 116(23): 265

[本文引用: 1]

[2]
Lee J H, Song Y J, Shin D H.
Microstructural evolution during superplastic bulge forming of Ti-6Al-4V alloy
[J]. Mater. Sci. Eng. A., 1998, 243(2): 119

[3]
Huang Z H, Qu HL, Deng C, et al.
Development and application of aerial titanium and its alloys
[J]. Mater. Rev., 2011, 25(1): 102

黄张�?/string-name>, 曲恒�?/string-name>, 邓超�?/etal>.
航空用钛及钛合金的发展及应用
[J]. 材料导报, 2011, 25(1): 102

[4]
Jin H X, Wei K X, Li J M, et al.
Research development of titanium alloy in aerospace industry
[J]. Chin. J. Nonferrous. Met., 2015, 25(2): 280

[本文引用: 1]

金和�?/string-name>, 魏克�?/string-name>, 李建�?/string-name>�?/etal>.
航空用钛合金研究进展
[J]. 中国有色金属学报, 2015, 25(2): 280

[本文引用: 1]

[5]
Yang B W, Xue Y, Zhang Y M, et al.
Study on high temperature deformation behavior of HIP TC4 titanium alloy
[J]. Hot. Working. Tech., 2018, 47(23): 46

[本文引用: 1]

杨博�?/string-name>, 薛勇, 张治�?/string-name>�?/etal>.
热等静压态TC4钛合金高温变形行为研�?/p> [J]. 热加工工�?/source>, 2018, 47(23): 46

[本文引用: 1]

[6]
Zhang Z M, Ren L Y, Xue Y, et al.
Microstructure of hot isostatically pressed Ti-6A1-4V alloy after hot deformation
[J]. Rare. Metal. Mat. Eng., 2019, 48(3): 820

[本文引用: 1]

张治�?/string-name>, 任璐�?/string-name>, 薛勇�?/etal>.
热等静压Ti-6Al-4V钛合金热变形微观组织演变
[J]. 稀有金属材料与工程, 2019, 48(3): 820

[本文引用: 1]

[7]
Hamed S, Langdon T G.
Using heat treatments,high-pressure torsion and post-deformation annealing to optimize the properties of Ti-6Al-4V alloys
[J]. Acta. Mater, 2017, 141: 419

[本文引用: 1]

[8]
Megumi K, Langdon T G.
The contribution of severe plastic deformation to research on superplasticity
[J]. Mater. Trans., 2019, 60(7): 1123

[9]
Kawasaki M, Figueiredo R B, Langdon T G.
Recent developments in the processing of advanced materials using severe plastic deformation
[J]. Mater. Sci. Forum., 2020, 72: 3304

[10]
Kawasaki M, Langdon T G.
Superplasticity in ultrafine-grained materials
[J]. Rev. Adv. Mater. Sci., 2018, 54(1): 46

[11]
Zhang S, Wang Y C, Zhilyaev A P, et al.
Temperature and strain rate dependence of microstructural evolution and dynamic mechanical behavior in nanocrystalline Ti
[J]. Mater. Sci. Eng. A., 2015, 641: 29

[本文引用: 1]

[12]
Zhang J Y.
Study on fine crystal heat treatment diagram and dynamic recrystallization behavior of TC4 titanium alloy
[D]. Xi'an: Xi'an University of Architecture and Technology, 2019

[本文引用: 2]

张君�?/string-name>.
细晶TC4钛合金的热加工图及动态再结晶行为研究
[D]. 西安: 西安建筑科技大学, 2019

[本文引用: 2]

[13]
Yang L Q, Yang Y Q.
Deformed microstructure and texture of Ti6Al4V alloy
[J]. T. Nonfree. Metal. Soc., 2014, 24(10): 3103

[本文引用: 2]

杨柳�?/string-name>, 杨延�?/string-name>.
Ti6Al4V钛合金的变形组织及织�?/p> [J]. 中国有色金属学报(英文�?, 2014, 24(10): 3103

[本文引用: 2]

[14]
Zhong X T, Huang L K, Wang L, et al.
A discontinuous dynamic recrystallization model incorporating characteristics of initial microstructure
[J]. T. Nonfree. Metal. Soc., 2018, 28(11): 2294

[本文引用: 1]

[15]
Hanlon D N, Sietsma J, Zwaag S V D.
The effect of plastic deformation of austenite on the kinetics of subsequent ferrite formation
[J]. Trans. Iron. Steel IOJ., 2001, 41(9): 1028

[本文引用: 1]

[16]
Estrin Y, Mecking H.
A unified phenomenological description of work hardening and creep based on one-parameter models
[J]. Acta. Metall., 1984, 32(1): 57

[本文引用: 1]

[17]
Poliak E I, Jonas J J.
A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization
[J]. Acta Mater., 1996, 44(1): 127

[本文引用: 1]

[18]
Mcqueen H J, Blum W.
Dynamic recovery: sufficient mechanism in the hot deformation of Al (<99.99)
[J]. Mater. Sci. Eng. A., 2000, 290(1-2): 95

[本文引用: 1]

[19]
Prasad Y V R K, Seshacharyulu T.
Processing maps for hot working of titanium alloys
[J]. Mater. Sci. Eng. A., 1998, 243(1~2): 82

[本文引用: 1]

Development of Ti-6Al-4V sheet with low temperature superplastic properties

1

2001

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

Microstructural evolution during superplastic bulge forming of Ti-6Al-4V alloy

0

1998

航空用钛及钛合金的发展及应用

0

2011

航空用钛及钛合金的发展及应用

0

2011

航空用钛合金研究进展

1

2015

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

航空用钛合金研究进展

1

2015

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

热等静压态TC4钛合金高温变形行为研�?/div>
1

2018

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

热等静压态TC4钛合金高温变形行为研�?/div>
1

2018

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

热等静压Ti-6Al-4V钛合金热变形微观组织演变

1

2019

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

热等静压Ti-6Al-4V钛合金热变形微观组织演变

1

2019

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

Using heat treatments,high-pressure torsion and post-deformation annealing to optimize the properties of Ti-6Al-4V alloys

1

2017

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

The contribution of severe plastic deformation to research on superplasticity

0

2019

Recent developments in the processing of advanced materials using severe plastic deformation

0

2020

Superplasticity in ultrafine-grained materials

0

2018

Temperature and strain rate dependence of microstructural evolution and dynamic mechanical behavior in nanocrystalline Ti

1

2015

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

细晶TC4钛合金的热加工图及动态再结晶行为研究

2

2019

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

... 等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

细晶TC4钛合金的热加工图及动态再结晶行为研究

2

2019

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

... 等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

Ti6Al4V钛合金的变形组织及织�?/div>
2

2014

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

... ,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

Ti6Al4V钛合金的变形组织及织�?/div>
2

2014

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

... ,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

A discontinuous dynamic recrystallization model incorporating characteristics of initial microstructure

1

2018

... Ti-6Al-4V合金是一�?i>α+β双相钛合金，具有高弹性模量、高韧性、低密度和良好的高温强度、抗蠕变和抗氧化性能，可用于制造航空武器装备的复杂结构零件^[1~4].近年来，随着航空武器装备性能指标的提高其关键部件、核心部位零件的结构设计日趋复杂.因此，用热成型加工实现Ti-6Al-4V合金复杂零件的一次性近净成形成为该领域的研究热点.杨博�?sup>[5]等进行高温热压缩实验建立了用于热等静压态Ti-6Al-4V合金高温流动行为的Arrhenius方程和DMM(动态材料模�?加工图，得到了这种合金加工性能与变形温度和应变速率的最优化匹配，并根据误差分析进一步证明了所建立的本构方程的预测准确�?张治�?sup>[6]等研究了变形温度和应变速率对Ti-6Al-4V合金显微组织的影响、分析了不同热变形参数下的组织特征，为制定热等静压态Ti-6Al-4V合金的后续锻造工艺提供了依据.Terence G. Langdon，R. C. Reed�?sup>[7~11]分别从Ti-6Al-4V合金超细晶制备和晶界调控方面开展了相关研究工作，在750~900℃温度区间得到了这种合金的最大超塑性延伸率�?15%�?200%，从而为其超塑成�?扩散连接技术的工程化应用奠定了基础.上述研究结果表明，Ti-6Al-4V合金在热成形加工过程中均发生了动态再结晶，是其具有良好热成形性能的关�?发生在低层错能合金中的动态再结晶(dynamic recrystallization, DRX)使合金内变形的晶粒和亚晶粒成为形核中心并演变为新的晶粒，是金属材料热变形的重要软化机�?因此，稳定化控制该合金锻造的工艺参数和动态再结晶组织，是提高Ti-6Al-4V合金锻造工艺水平的共性科学问题之一.为此，张君彦^[12]结合对应加工区间的合金组织图分析了变形机理，根据对实验结果的分析阐述了动态再结晶行为；YANG^[13]等研究动态再结晶时发现，亚晶界吸收了位错并在高角度晶界生成了再结晶晶粒；Xi^[14]等为了定量描述和预测堆垛层错能的金属在热加工过程中的不连续动态重结晶(DDRX)的动力学过程，提出了一种新的基于物理学的模型，进行了旨在提供动力学数据(例如再结晶晶粒的尺寸和体积分�?和相关微结构的实验，取得了模型预测与实验结果的良好一致性并在此基础上阐明了与再结晶晶粒生长有关的热动力学关�?本文在文献[12,13]的基础上进行Ti-6Al-4V合金的单道次热压缩实验，在KM模型的基础上描述其动态再结晶流变应力并应用Poliak-Jonas准则分析动态再结晶临界应变条件，基于Avrami模型揭示动态再结晶体积分数的演化规律并将动态再结晶力学行为、组织转变体积分数等参数引入功率耗散率模型得到动态再结晶过程的能量变化规�?最后，使用TEM表征Ti-6Al-4V合金的微观组织验证模型化理论结果并揭示其动态再结晶行为. ...

The effect of plastic deformation of austenite on the kinetics of subsequent ferrite formation

1

2001

... 从能量角度分析，该合金的热变形过程是一个热激活过程，流变应力与变形工艺参数间满足Arrhenius本构关系模型^[15] ...

A unified phenomenological description of work hardening and creep based on one-parameter models

1

1984

... Poliak和Jonas^[16]认为，发生动态再结晶时应变与应力之间的关系为 ...

A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization

1

1996

... Avrami提出了金属材料动态再结晶过程中动力学转变经典模型^[17] ...

Dynamic recovery: sufficient mechanism in the hot deformation of Al (<99.99)

1

2000

... 其中ε为应变值；ε_c为临界应变量�?i>ε_p为峰值应力应变量；K₁，K₂为常数；X_d为动态再结晶分数.据文献[18]�?i>ε_c< ε_p< ε_s�?i>X_d与流变应力之间的关系�?...

Processing maps for hot working of titanium alloys

1

1998

... 从物理学角度，金属材料发生动态再结晶时伴随着能量的转�?P)，包括材料发生变形需要的能量(G)和组织演变消耗的能量(J).发生动态再结晶组织转变势必引起原子势能的变化，而变形过程中位错运动、晶界滑移等则以热量形式耗散.因此，根据Prasad^[19]等人提出的耗散结构理论模型 ...

/

�? �?

版权所有 © 2017 《材料研究学报》编辑部
地址: 沈阳市文化路72号, 中国科学院金属研究所(110016)
电话: +86-024-23971297，传真: +86-024-83978072，E-mail: cjmr@imr.ac.cn，http://www.cjmr.org
本系统由北京玛格泰克科技发展有限公司设计开发技术支持：support@magtech.com.cn

Ti-6Al-4V合金热压缩过程中的动态再结晶

Dynamic Recrystallization of Ti-6Al-4V Alloy During Hot Compression

1 实验方法

2 实验结果

2.1 Ti-6Al-4V合金的热变形本构关系

�?

2.2 Ti-6Al-4V合金动态再结晶的物理模�?

�?

�?

�?

2.3 Ti-6Al-4V合金的动态再结晶能量耗散模型

�?

2.4 Ti-6Al-4V合金的动态再结晶显微组织

�?

�?

3 结论

参考文�?

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

Parameters	Value	Parameters	Value
b₀	-12.9616	b₅	0.48118
b₁	-0.5318	b₆	0.03365
b₂	-0.05727	b₇	23.7294
b₃	0.0309	b₈	1.02584
b₄	0.81679

Strain rate/s^-1	ε_c
Strain rate/s^-1	870�?/th>	900�?/th>	930�?/th>	960�?/th>
5×10^-4	0.3089	0.2936	0.2724	0.2536
1×10^-3	0.3177	0.2991	0.2872	0.2701
5×10^-3	0.3302	0.3156	0.3007	0.2841
5×10^-2	0.3498	0.3301	0.3191	0.2951

Ti-6Al-4V合金热压缩过程中的动态再结晶

Dynamic Recrystallization of Ti-6Al-4V Alloy During Hot Compression

1 实验方法

2 实验结果

2.1 Ti-6Al-4V合金的热变形本构关系

�?

2.2 Ti-6Al-4V合金动态再结晶的物理模�?

�?

�?

�?

2.3 Ti-6Al-4V合金的动态再结晶能量耗散模型

�?

2.4 Ti-6Al-4V合金的动态再结晶显微组织

�?

�?

3 结论

参考文�? View Option 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

参考文�?

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子