基于动态再结晶37CrS4特种钢的流变应力预测模型

图1 37CrS4钢的原始金相组织

Fig.1 Original microstructure of 37CrS4 steel

2 实验结果

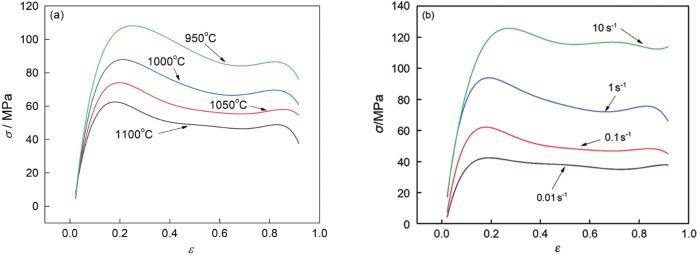
图2给出了37CrS4钢应变速率为0.1s^-1时的真应力应变曲线(图2a)和温度为1100℃的真应力应变曲线(图2b)以便进行横向、纵向对比。真应力应变曲线均经过摩擦修正和插值，将其拟合为平滑的曲线。可以看出，应变速率为0.1 s^-1时不论温度高低真应力应变曲线都出现了较为明显的峰值点，且温度越高峰值点对应的应变值越低。因为温度越高峰值应力越小，应力峰值将在热压缩变形量越少的地方产生，随后出现应力降低。根据相关金属热塑性变形理论，此时动态再结晶(DRX)行为占主导。DRX的微观本质是再结晶晶粒的生成和长大过程，通过消除金属微观组织内部的位错、畸变等缺陷使热压缩产生的变形抗力软化。此时，动态软化占主导地位^[1]。图2a中在所有温度下都出现动态软化，说明37CrS4钢在应变速率为0.1 s^-1时的热变形都发生了较为明显的动态再结晶。

图2

图2 37CrS4钢的真应力应变曲线

Fig.2 True stress-strain curve of 37CrS4 steel of 0.1 s^-1 with different temperatures (a) and at 1100℃ with different stain rates (b)

图2b给出了温度为1100℃时的真应力随应变的变化。可以看出，应变速率为10 s^-1时虽然发生了DRX软化，但是由于应变速率过高热变形很快进入二次硬化阶段。在整个热变形过程中DRX进行得不完全，较高的应变速率限制了热变形行为。其原因是，金属微观组织中位错的形成与变形量相关。较高的应变速率使变形量极快增加和位错密度的提高，而DRX的速率并不受应变速率影响，因此大量的位错不能被DRX消除，加工硬化占据主导，真应力应变曲线偏向于动态回复(DRV)。应变速率类似于温度对DRX行为的影响，应变速率越低则峰值应力越小，峰值应力对应的应变越小。

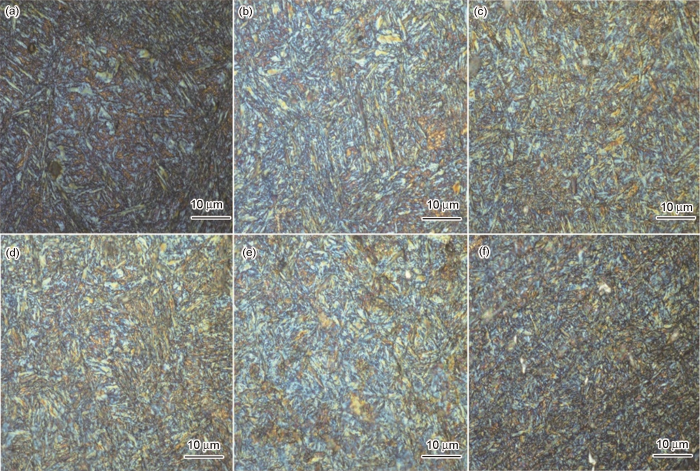
图3给出了37CrS4钢在950~1100℃、应变速率为0.01 s^-1~10 s^-1时热变形微观组织演变的金相组织照片。图3a、图3b、图3c分别给出了在1100℃应变速率为0.01 s^-1~10 s^-1的情况。可以看出，发生了较为明显的DRX现象，微观组织为板条状马氏体，未见碳化物。原有的奥氏体晶界已经破碎，在温度相同的情况下应变速率依次增大，在1100℃、0.01 s^-1的条件下奥氏体晶粒不断长大，马氏体相变也比较充分(图3a)。图3b和图3c表明，在应变速率较高的情况下奥氏体中产生了大量位错，而马氏体相变继承母相的晶体缺陷加重这一趋势，使马氏体相变后位错大量积累，使流变应力再度增大。而图3d~f表明，在应变速率为0.1 s^-1的情况下，温度越高则马氏体越完整，温度越低则马氏体边缘越弯曲，甚至出现断裂。其原因是，温度越低DRX晶粒越小，妨碍了马氏体的形核和长大。

图3

图3 37CrS4钢的热变形微观组织金相照片

Fig.3 Metallographic diagram of microstructure during hot deformation of 37CrS4 in the conditions of at 1100℃, stain rates 0.01 s^-1 (a), 1 s^-1 (b), 10 s^-1 (c) and stain rates 0.1 s^-1, at 1050℃ (d), at 1000℃ (e), at 950℃ (f)

3 分析讨论

3.1 DRX临界应变模型的建立

根据热变形加工硬化的相关理论^[16]，引入加工硬化率参数

θ = \frac{d σ}{d ε}

(1)

式中σ为真应力，MPa；ε为真应变。

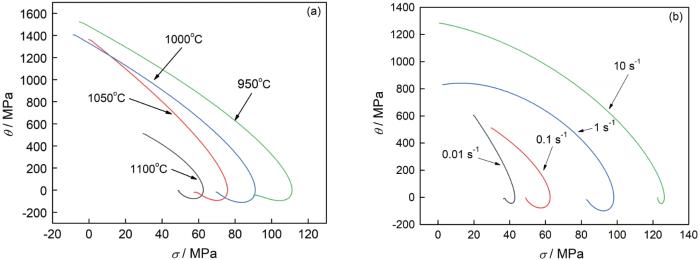
图4给出了根据图2中的真应力应变曲线计算出的加工硬化曲线。图4表明，每条曲线都有一个应力最大值。应力最大值点，对应峰值应力σ_p。根据金属材料DRX理论^[1]，金属的DRX行为在达到峰值应力之前就开始了。其原因是，在热变形过程中位错引起的加工硬化与动态软化相互竞争，峰值应力的出现意味着DRX引发的软化行为在与加工硬化的竞争中占据优势，宏观真应力应变曲线出现起伏，DRX引起的软化行为的开始必然早于峰值应变ε_p(峰值应力σ_p对应的应变值)。但是，从金属热变形微观组织里难以找到DRX开始时参数的临界值。Poliak和Jonas^[17]的工作表明，可避开难以进行的实验测量，直接从加工硬化曲线得出结论：当曲线随着应力不断增大而加工硬化率不断降低出现“拐点”(二阶导数值为0)时，表明DRX行为开始发生。图4a和图4b表明，加工硬化图像均未出现明显的“拐点”，说明直接对所有范围内的真应力应变曲线采用七次多项式拟合加工硬化，其精度不能满足反映局部图像细节变化的条件。

图4

图4 37CrS4钢的加工硬化曲线

Fig.4 Work hardening curve of 37CrS4 steel in conditons of 0.1 s^-1with different temperatures (a) and at 1100℃ with different stain rates (b)

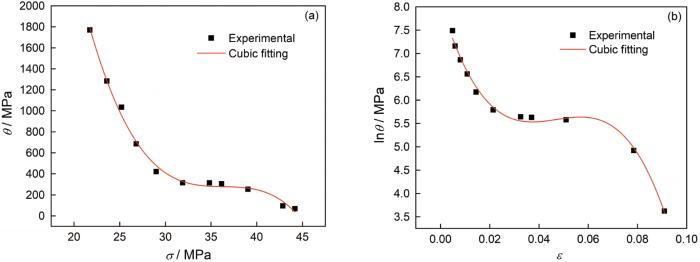
由于Gleeble-1500D能反映任意时刻应力应变的变化，为了捕捉“拐点”的精确位置，放大了拐点所在的区域。根据DRX理论，DRX行为在峰值应变之前就已经开始并产生作用，因此选择考察区域时应变值右端不应超过峰值应变^[2]。局部放大的临界应变值与临界应力值，可只考察细节区域的三次拟合函数的“拐点”。选择三次多项式拟合，一方面能描述加工硬化率与应力应变的关系^[18]，另一方面三次多项式有唯一的“拐点”，能满足临界应变的定义对加工硬化曲线的要求。根据图4b中温度为1100℃、应变速率0.01 s^-1时的曲线，得到局部加工硬化应力应变散点并由三次多项式拟合。如图5a所示，该三次多项式的形式为

θ = P_{1} σ^{3} + P_{2} σ^{2} + P_{3} σ + P_{4}

(2)

其中P₁、P₂、P₃、P₄为θ-σ散点拟合的三次多项式对应的三次项、二次项、一次项、常数项系数。将三次多项式对σ求二阶导数，可得

\frac{d^{2} θ}{d σ^{2}} = 6 P_{1} σ + 2 P_{2}

(3)

DRX开始时，(3)式值为0时的σ值即为临界应力值，于是得

\frac{d^{2} θ}{d σ^{2}} = 6 P_{1} σ_{c} + 2 P_{2} = 0

(4)

即

σ_{c} = - \frac{P_{2}}{3 P_{1}}

(5)

不能根据θ-ε曲线求解临界应变，因为应变值ε与加工硬化θ的差距为4~5个数量级，过大的数值差使临界应变数值解的误差过大。针对这种情况，可考察lnθ-ε曲线的拐点以避免误差过大。温度为1100℃、应变速率为0.01 s^-1的lnθ-ε曲线，如图5b所示。将加工硬化率对数化，可避免数量级差距大，对应的三次多项式为

l n θ = K_{1} ε^{3} + K_{2} ε^{2} + K_{3} ε + K_{4}

(6)

其中K₁、K₂、K₃、K₄为lnθ-ε散点拟合的三次多项式对应的三次项、二次项、一次项、常数项系数。与临界应力的求解方法类似，临界应变的解为

ε_{c} = - \frac{K_{2}}{3 K_{1}}

(7)

图5表明，散点与拟合曲线的相关性R²=0.9765。拟合精度较高，说明三次多项式拟合方法正确。在其他温度、应变速率情况下，计算临界应力、临界应变的方法相同。将临界应变与峰值应变分别绘制二维散点图，可见37CrS4的临界应变与峰值应变均存在线性关系，如图6所示。

图5

图5 在1100℃、0.01 s^-1条件下37CrS4钢的加工硬化率与应力应变的三次拟合关系

Fig.5 θ-σ curve (a)andlnθ-ε curve (b) in conditions of 1100℃、0.01 s^-1 cubic fitting relationship between work hardening rate and stress-strain for 37CrS4 steel

图6

图6 37CrS4钢的临界应变模型线性拟合关系

Fig.6 Linear fitting relationship of critical strain model of 37CrS4 steel

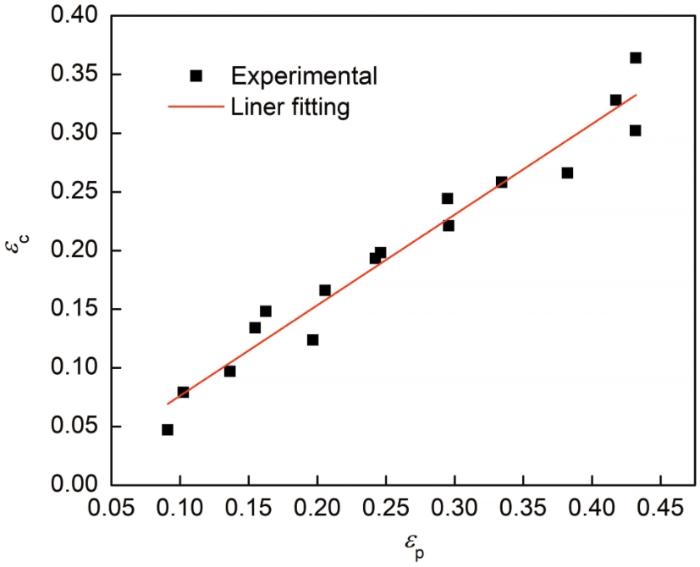
由于线性拟合后的直线截距很小，数量级为10^-4，可以忽略不计，线性拟合相关度R²=0.9576。由此可得37CrS4钢的临界应变模型

ε_{c} = 0.77162 ε_{p}

(8)

3.2 DRX模型的建立

3.2.1 Zener-Hollomon参数

Sellars建立的用双曲正弦函数修正的Arrhenius本构模型，可表征金属材料的应力应变特性^[18]。双曲正弦修正的Arrhenius本构方程为

ε' = A F (σ) e x p \frac{Q}{R T}

(9)

式中Q为热变形激活能kJ/mol；F(σ)为应力σ的函数；R为气体常数(8.314 J/mol)；T为温度/℃；α、A为材料常数；ε'为应变速率/s^-1。

依据37CrS4钢热压缩实验的峰值应力数据和使用MATLAB编程，可求解各项材料常数^[19,20]。结果表明，各项材料常数为α=0.008，n=5.765，Q=293 kJ/mol，A=4.46×10⁹。Zener-Hollomon参数(Z参数)是Zener和Hollomon等提出的一项重要参数，即热力学补偿因子^[20]，Z参数的表达式为

Z = ε' e x p \frac{Q}{R T} = A [s i n h {(α σ)]}^{n}

(10)

将Q值代入如(10)即可计算出不同应变速率、温度下的Z值。

3.2.2 DRX体积分数模型的建立

根据DRX运动学理论，DRX的体积分数模型可以用Johnson-Mehl-Avrami(JMA)方程^[17]

X_{d} = 1 - e x p [- m_{1} {(\frac{ε - ε_{c}}{ε_{p}})}^{m_{2}}]

(11)

表达，式中X_d为DRX体积分数值，m₁、m₂为材料常数值。

可用线性回归方法，根据已有的体积分数与相应的应变数据得到散点，再用拟合方法求出材料常数m₁、m₂。求解各种温度、应变速率对应的DRX体积分数的方法是，找出DRX体积分数与真应力应变曲线之间的联系，建立相应的数学模型估计任一变形量下的DRX体积分数值^[16]

X_{d} = \frac{σ_{s a t} - σ}{σ_{s a t} - σ_{s s}}

(12)

式中σ_sat为饱和应力，σ_ss为稳态应力。

假设材料热变形不发生DRX，饱和应力σ_sat是流变应力随应变量累积的变化，可根据加工硬化曲线估算饱和应力。过加工硬化曲线的“拐点”(临界应变出现的点)做切线，其与直线θ=0的交点即为饱和应力σ_sat。稳态应力是指，DRX的软化行为与加工硬化行为的“竞争”逐渐落入“下风”，发生二次硬化时流变应力开始从逐渐变小变为逐渐降低临界点，对应θ-σ曲线第二次与θ=0的直线相交时的应力值，为稳态应力σ_ss。为了得到体积分数散点，按照真应变0.1~0.9分别取值，步长为0.1，计算对应的DRX体积分数。值得注意的是，由于临界应变的影响，部分低温、高应变速率的DRX在待测应变处尚未发生DRX行为，所以需要将无DRX发生的应变取值点舍弃。将式(11)两边取两次对数，得

l n [- l n (1 - X_{d})] = m_{2} l n (\frac{ε - ε_{c}}{ε_{p}}) - l n m_{1}

(13)

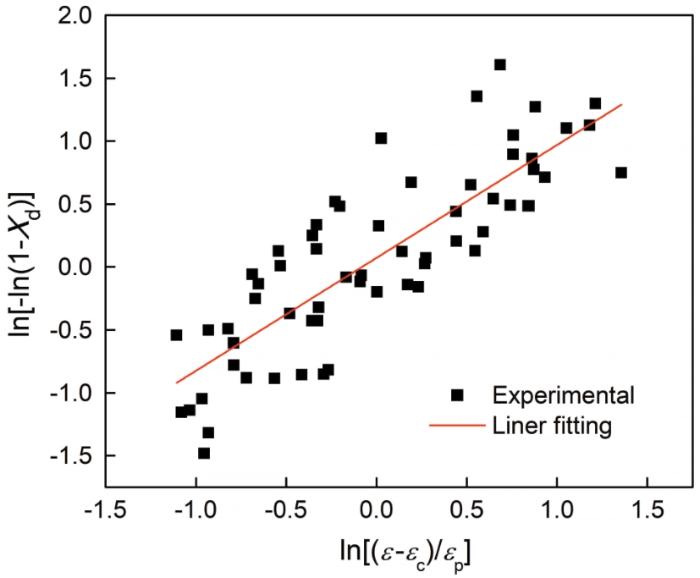
根据已有的DRX体积分数散点进行线性拟合(图7)，得到的直线斜率为m₂，截距为-lnm₁。DRX体积分数散点的分布基本呈现线性关系，但偏离拟合直线较多。其原因是，DRX体积分数散点是包含多种温度、应变速率条件的散点集合。根据已有的DRX体积分数散点进行线性拟合，得到如图7所示的图像，拟合得到的直线斜率为m₂，截距为-lnm₁。将所有体积分数散点同时求拟合的直线，相比分别拟合求直线截距、斜率均值，减少了中间环节带来的误差。结果表明，m₂=0.89743，-lnm₁=0.7193，得到DRX体积分数模型

X_{d} = 1 - e x p [- 2.053 {(\frac{ε - ε_{c}}{ε_{p}})}^{0.89743}]

(14)

图7

图7 ln[-ln(1-X_d)]与ln[(ε-ε_c)/ε_p]的线性关系

Fig.7 Linear relationship between ln[-ln(1-X_d)] and ln[(ε- ε_c)/ε_p]

3.3 基于DRV、DRX的分段式本构模型的建立和验证

3.3.1 分段式本构模型的建立

在热压缩变形的初始阶段，位错密度随着加工硬化的增加而提高。动态回复使组织内的点缺陷修复和位错密度的进一步提高，位错密度的变化为^[18]

\frac{d ρ}{d ε} = U - Ω ρ

(15)

式中ρ为位错密度；U为加工硬化系数；Ω为动态软化系数。热变形时，位错密度与真应力之间的关系为^[16]

σ = α μ b \sqrt[]{ρ}

(16)

式中α为材料常数；μ为剪切模量；b为Burgers矢量；将式(14)代入式(13)并积分可得DRV阶段本构方程^[13]

σ_{D R V} = [{σ_{s a t}}^{2} + ({σ_{0}}^{2} - {σ_{s a t}}^{2}) e x p {(- Ω ε)]}^{0.5}

(17)

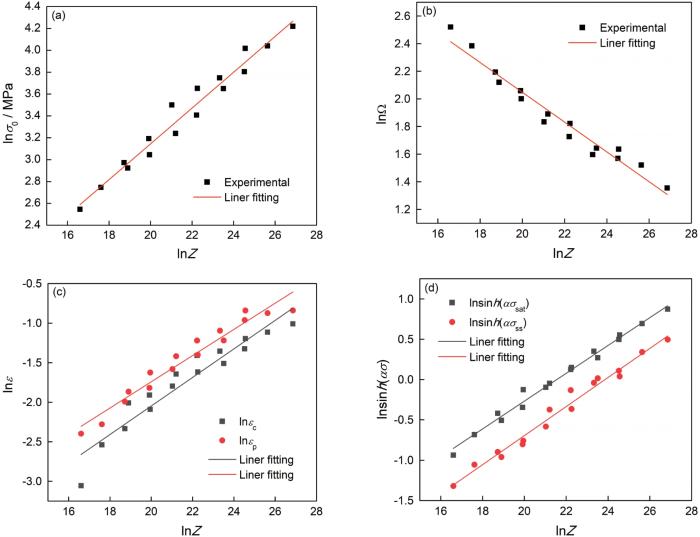
式中σ₀为屈服应力。根据真应力应变曲线0.2%处的直线与真应力应变曲线的交点可求得用Z参数表征的σ₀。由于σ₀与Z的数量级差距较大，σ₀、Z需要对数化建立线性拟合关系。本文用的是低应力水平的对应关系，因为屈服应力值的波动处在较低的应力范围内。用低应力水平的应力应变对应关系比较合适σ₀与Z之间的线性拟合关系。如图8a所示，lnσ₀与lnZ的关系为

l n σ_{0} = 0.16374 l n Z - 0.13027

(18)

图8

图8 材料参数的对数与lnZ间的线性拟合关系

Fig.8 Linear fitting relationship between the logarithm of material parameters and lnZ (a) lnZ with lnΩ; (b) lnZ with lnσ₀; (c) lnZ with lnε_cand lnε_p; (d) lnZ with lnsinh(ασ_sat)and lnsinh(ασ_ss)

和

σ_{0} = 0.877858 Z^{0.16374}

(19)

根据

Ω = \frac{1}{ε} l n \frac{{σ_{0}}^{2} - {σ_{s a t}}^{2}}{σ^{2} - {σ_{s a t}}^{2}}

(20)

可求解动态软化系数Ω^[13]。用Z参数表征Ω在各温度、应变速率下的散点值，lnΩ与lnZ之间的线性关系如图8b所示。拟合直线方程可得lnΩ与lnZ 以及Ω-Z的关系

l n Ω = - 0.16795 l n Z + 4.20705

(21)

Ω = 67.15813 Z^{- 0.16795}

(22)

变形进行到临界应变点时37CrS4钢开始发生DRX行为，DRV、DRX、加工硬化共同作用，结合DRX体积分数的关系式可得DRX阶段的本构方程^[14]

σ_{D R X} = σ_{s a t} - (σ_{s a t} - σ_{s s}) X_{d}

(23)

DRX体积分数含有临界应变、峰值应变，与屈服应力、动态软化系数相同，都可用Z参数表征。如图8c所示，临界应变、峰值应变与Z参数之间的关系为

\{\begin{array}{l} l n ε_{c} = 0.18041 l n Z - 5.6559 \\ l n ε_{p} = 0.16567 l n Z - 5.05544 \end{array}

(24)

由式(24)可得临界应变，峰值应变的Z参数可表示为

\{\begin{array}{l} ε_{c} = 0.0035 Z^{0.18041} \\ ε_{p} = 0.0064 Z^{0.16567} \end{array}

(25)

此时还需将饱和应力σ_sat和稳态应力σ_ss统一表示，Z参数也能表征σ_sat、σ_ss，但是与屈服应力不同。σ_sat、σ_ss应力分布在高、低应力水平，用σ或lnσ都不能准确描述。应该使用适合所有应力情况的双曲正弦形式描述饱和应力与稳态应力，如图8d所示，其中稳态应力、饱和应力的关系为

\{\begin{array}{l} l n s i n h (α σ_{s a t}) = 0.17248 l n Z - 3.71718 \\ l n s i n h (α σ_{s s}) = 0.18021 l n Z - 4.29965 \end{array}

(26)

由式(22)可得用Z参数表示的临界应变和峰值应变，即

\{\begin{array}{l} σ_{s a t} = 124.8752 s i n h^{- 1} (0.0243 Z^{0.17248}) \\ σ_{s s} = 124.8752 s i n h^{- 1} (0.0136 Z^{0.18021}) \end{array}

(27)

综上所述，基于DRX模型与位错密度理论的本构模型为

\{\begin{array}{l} σ_{D R V} = [{σ_{s a t}}^{2} + ({σ_{0}}^{2} - {σ_{s a t}}^{2}) e x p {(- Ω ε)]}^{0.5} (ε < ε_{c}) \\ σ_{D R X} = σ_{s a t} - (σ_{s a t} - σ_{s s}) X_{d} (ε \geq ε_{c}) \\ X_{d} = 1 - e x p [- 2.053 {(\frac{ε - ε_{c}}{ε_{p}})}^{0.89743}] \\ ε_{c} = 0.0035 Z^{0.18041} \\ ε_{p} = 0.0064 Z^{0.16567} \\ σ_{s a t} = 124.8752 s i n h^{- 1} (0.0243 Z^{0.17248}) \\ σ_{s s} = 124.8752 s i n h^{- 1} (0.0136 Z^{0.18021}) \\ Ω = 67.15813 Z^{- 0.16795} \\ σ_{0} = 0.877858 Z^{0.16374} \\ Z = ε' e x p \frac{293000}{8.314 T} \end{array}

(28)

3.3.2 分段式本构模型预测能力的验证

为了测试基于DRX的本构模型对37CrS4钢的预测能力和考察模型的预测精度，对照分析了应变速率为0.1 s^-1和温度为1100℃在所有应变速率情况下的结果，如图9所示。由图9可见，分段式本构模型的平均相关度R²=0.9756，表明其预测能力较强、精度较高。

Fig.9 Comparison of model predicted stress and test value (a) at different temperatures and strain rate is 0.1 s^-1, (b) at 1100℃ and different stain rates

4 结论

(1) 37CrS4钢在温度为950~1100℃、应变速率为0.01 s^-1~10 s^-1条件下发生动态再结晶行为，且温度越高、应变速率越低动态再结晶行为越早发生。在高应变速率条件下二次硬化较早发生，使DRX行为不明显。用分段式的流变应力预测模型可预测37CrS4钢的流变应力变化。热变形结束后钢的金相组织为板条状马氏体，其塑性和强度良好。

(2) 基于动态再结晶动力学理论引入Z参数表征临界应变、峰值应变，构建了37CrS4钢的DRX临界应变模型 $ε_{c} = 0.77162 ε_{p}$ ，再根据稳态应力、饱和应力和Z参数之间的线性关系进行线性拟合可得到峰值应变的DRX体积分数模型 $X_{d} = 1 - e x p {- 2.053 [(ε - ε_{c}) / ε_{p}]^{0.897}}$ 。

(3) 使用基于动态再结晶模型和位错密度理论建立的37CrS4钢关于DRV、DRX的分段式本构模型，对性能的预测值与实验值的相关度达到0.9756，验证了分段式本构模型的正确性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Tian

Y X

, Liu

, Cao

H L

, et al.

Research progress of dynamic recrystallization of metallic materials

[J]. Rare Metal Mat. Eng., 2019, 48(11): 3764

田宇兴, 刘成, 曹海龙等.

金属材料的动态再结晶研究进展

[J]. 稀有金属材料与工程, 2019, 48(11): 3764

[2]

Sun

, Zhou

, Wan

Z P

, et al.

Research status of dynamic recrystallization model of metallic materials

[J]. Mater Rev, 2017, 31 (13): 12

孙宇, 周琛, 万志鹏等.

金属材料动态再结晶模型研究现状

[J]. 材料导报, 2017, 31(13): 12

[3]

W J

, Yang

X R

, Luo

, et al.

Dynamic recrystallization model of ultrafine grained pure titanium with composite deformation

[J]. Chin. J. Mater. Res., 2020, 34(03): 217

马炜杰, 杨西荣, 罗雷等.

复合形变超细晶纯钛的动态再结晶模型

[J]. 材料研究学报, 2020, 34(03): 217

[4]

Cao

, Di

H S

, Zhang

J C

, et al.

Dynamic recrystallization behavior of 800H alloy

[J]. Acta Metall. Sin., 2012, 48(10): 1175

曹宇, 邸洪双, 张洁岑等.

800H合金动态再结晶行为研究

[J]. 金属学报, 2012, 48(10): 1175

[5]

Bai

Y B

Study on the forming and microstructure change of 30CrMoA thin-walled cylindrical parts

[D]. Qinghuangdao: Yanshan University, 2018.

白英博

30CrMoA薄壁筒形件成形及微观组织变化研究

[D]. 秦皇岛: 燕山大学, 2018

[6]

Eli

S P

, Jean

, Mirentxu

, et al.

Constitutive description for the design of hot-working operations of a 20MnCr5 steel grade

[J]. Mater. Des., 2014, 62: 255

[7]

Illarionov

A G

, Trubochkin

A V

, Shalaev

A M

, et al.

Isothermal de-composition of β-Solid solution in titanium Alloy Ti-10V-2Fe3Al

[J]. Met. Sci. Heat Treat., 2017, 58: 674

[8]

Mejía

, Reyes Calderón

, Cabrera

J M

Modeling the hot flow behavior of a Fe-22Mn-0.41C-1.6Al-1.4Si TWIP steel micro alloyed with Ti, V and Nb

[J]. Mater. Sci. Eng. A, 2015, (644): 374

[9]

Liu

S P

, Li

D F

, Guo

S L

Critical conditions of dynamic recrystallization for B4Cp/6061Al composite

[J]. Rare Metal Mat. Eng.,2017, 46(07): 1815

[10]

Ouyang

D L

, Cui

, Lu

S Q

, et al.

Compression deformation behavior and dynamic recrystallization in β phase region of forged TB6 titanium alloy

[J]. Chin. J. Mater. Res., 2019, 33(03): 218

欧阳德来, 崔霞, 鲁世强等.

锻态TB6钛合金β相区压缩变形行为和动态再结晶

[J]. 材料研究学报, 2019, 33(03): 218

[11]

Ouyang

D L

, Lu

S Q

, Cui

, et al.

Dynamic recrystallization kinetics of β-zone deformation of TB6 titanium alloy

[J]. A Chin. J. Mater. Res., 2019, 33(12): 918

欧阳德来, 鲁世强, 崔霞等.

TB6钛合金β区变形的动态再结晶动力学

[J]. 材料研究学报, 2019, 33(12): 918

[12]

Zhao

, Zhong

, Yan

, et al.

Deformation behaviour and mechanisms during hot compression at supertransus temperatures in Ti10V-2Fe-3Al

[J]. J. Alloy. Compd., 2017(02), 710

[13]

Wang

M H

, Wang

G T

, Yue

Z M

, et al.

Hot deformation behavior and constitutive model of 20MnNiMo steel

[J]. J SHANGHAIJIAOTONG U, 2016, 50(07): 1041

王梦寒, 王根田, 岳宗敏等.

20MnNiMo钢热变形行为及基于物象的本构模型

[J]. 上海交通大学学报, 2016, 50(07): 1041

[14]

Study on thermoplastic deformation behavior of GH4698 nickel base superalloy

[D]. Harbin: Harbin Institute of technology, 2015.

胡超

GH4698镍基高温合金热塑性变形行为研究

[D]. 哈尔滨: 哈尔滨工业大学, 2015

[15]

Chen

X W

, Wang

J Y

, Yang

X Q

, et al.

Hot deformation behavior and dislocation density evolution of Cr8 alloy steel

[J]. J.JILIN. U.

: TECHNO

ED., 2020, 50(01): 91

陈学文, 王继业, 杨喜晴等.

Cr8合金钢热变形行为及位错密度演变规律

[J]. 吉林大学学报(工学版), 2020, 50(01): 91

[16]

Puchi-Cabrera

E S

, Guérin

J D

, La

J G

, et al.

Incremental constitutive description of SAE5120 steel deformed under hot-working conditions

[J]. Int. J. Mech. Sci., 2017, 133: 619

[本文引用: 4]

[17]

Chen

Y Z

, Pang

Y H

, Wang

J G

, et al.

Hot deformation constitutive equation of GH2907 alloy

[J]. Rare Metal Mat. Eng., 2019, 48 (11): 3577

陈益哲, 庞玉华, 王建国等.

GH2907合金热变形本构方程

[J]. 稀有金属材料与工程, 2019, 48(11): 3577

[18]

, Mi

Z L

, Li

, et al.

Hot deformation constitutive model of ultra high strength dual phase steel dp1000 based on dislocation density theory

[J]. A Chin. J. Mater. Res., 2017, 31(08): 576

徐梅, 米振莉, 李辉等.

基于位错密度理论的超高强双相钢DP1000热变形本构模型

[J]. 材料研究学报, 2017, 31(08): 576

[19]

Quan

S J

, Song

K X

, Zhang

Y M

, et al.

Hot deformation behavior and hot working diagram of Ti80 alloy based on MATLAB

[J]. Rare Metal Mat. Eng., 2019, 48(11): 3600

权思佳, 宋克兴, 张彦敏等.

基于MATLAB的Ti80合金热变形行为及热加工图

[J]. 稀有金属材料与工程, 2019, 48(11): 3600

[20]

Zhang

Q H

, Su

J H

, Zhang

X B

, et al.

High temperature deformation behavior and constitutive equation of as cast C19400 alloy based on MATLAB

[J]. T. Mater. Heat Treat., 2019, 40(08): 161

张启航, 苏娟华, 张学宾等.

基于MATLAB的铸态C19400合金高温变形行为及本构方程

[J]. 材料热处理学报, 2019, 40(08): 161