与不同双态组织特征相关的力学性能的差异,主要来自于在变形过程中组织内部多相间的力学相互作用(空间应力、应变分布及相间应力、应变分配)。由于多相及形态共存空间应力、应变分布,双态组织使其微观应力应变分布复杂,甚至在同一相内的分布也不均匀[7,8]。但是,用常规实验方法难以表征其内部应力应变分布的特征。虽然近年来纳米压痕可给出不同晶粒取向时的硬度和模量[9],也有基于EBSD点阵畸变计算应力应变场[10],但是二者都有较大的局限性,特别是在发生较大塑性变形时难以估计晶体取向和缺陷密度。用宏观有限元方法研究多相材料的力学行为,多集中于双相材料而忽视了单晶弹塑性各向异性且无法描述包含位错等作用的变形特征[7,11,12,13]。介观层面的晶体塑性有限元方法,可采用Voronoi图法生成等轴组织,但是无法描述双态组织中βT片层特征结构。曾有人将βT简化为单晶体进行研究[14],但是无法考虑片层内部αs和β之间的相互力学作用和应力应变分布差异。而实验研究结果表明,裂纹常见于αs和β之间[15,16]。几何模型可逼近真实组织的特征[17],但是其βT中的单变体结构与实际组织中常见的多变体的特征不同。关于应力应变分配研究,目前应用广泛的分配系数公式[18]是结合单相和多相应力应变曲线拟合得到的,在给定相类型和比例条件下其数值即确定,无法描述不同组织特征条件下应力应变的差异性分配。实际上,在不同合金的多相组织变形中都存在空间应力应变分布和分配问题,并且变形后普遍存在不均匀和非协调现象,而组织变形后的协调性特征描述性居多,定量化评估匮乏,亟待进一步研究。本文基于滑移为主的率相关晶体塑性有限元方法创建βT中包含多变体结构特征的几何模型,以应用广泛的Ti-6Al-4V合金为例[19],通过控制双态组织特征应用提出一种变形协调性的定量统计方法以研究不同初生α相体积分数、αs片层厚度、βT中变体类型数目以及对合金高温变形行为的影响,重点关注空间应力应变分布特征、各相应力应变分配和变形协调性规律。最后基于双态组织变形过程中不同相应力应变响应特征,对合金的组织控制提出理论建议。
1 模拟方法
1.1 率相关晶体塑性模型
晶体塑性理论,从位错滑移出发对变形后单晶体内离散分布的位错进行均匀化处理,从而实现晶体变形运动学在连续介质力学的描述,进而推导出包含晶体变形物理机制的单晶或多晶弹塑性本构方程[20,21,22,23]。基于此框架,晶体塑性理论建立了微观材料变形机制同宏观变形行为的联系,根据不同的研究问题发展出多方面的模型,如包含孪生变形机制[24,25,26]、疲劳[27,28]、剪切带[29,30]等。在变形运动学中速度梯度塑性变形部分
式中
式中
1.2 应力应变分配及协调性统计方法
多晶变形后其应力应变分布,不仅在空间上整体或局域存在差异性分布特征,而且组织中不同相类型的分配也有明显的差异。关于多晶中不同相应力应变分配国内外有大量研究并主要集中于双相材料,其应力应变曲线的简化有通过单相力学性能基于混合法则获得的[34],深入一点的通过单相力学性能宏观有限元计算获得[7]。这两种方法都具有快捷的特征,但是存在一定的局限性。简化混合法则存在误差并几乎无法避免;宏观有限元假设单相晶粒各向同性,对于弹塑性各项异性明显材料的描述准确度不够。常见的应力应变分配系数公式[18],难以表达不同组织特征条件下应力应变分配的差异性。以滑移控制为主的晶体塑性有限元结合了精细逼近微观组织特征的几何构型,可避免宏观层面评估粗略和原子层面样本的不足,获得“中间”的平衡。
对于钛合金双态组织,实验上主要观察到初生α相(αp),次生α相(αs)和β相。其应力应变分配主要通过数理统计方法获得,采用公式(4)中统计三种相类型的平均值,对比其大小和变化即可得到应力应变整体性平均值的差异。这种应力应变分配不均表征了变形非协调现象,但是目前对多晶变形协调性定量化的评估未见报道。本文从统计学中延伸,提出一种度量方法。公式(4)中的平均值μ和标准差σ无法评估不同样本(数据类型和数目)的数据集偏离中心的离散程度,变异系数CV(Coefficient of Variation)可避免该问题。对于应力和应变统计对象,变异系数CV取值多数情况为[0,1],数值越高表明数据非一致性程度越高,而数据变异性对应的相反状态表征了数据的协调一致性。因此,本文依据变异系数对应内涵和取值范围提出采用公式(5)来定义变形协调系数CC(Coefficient of Consistency)。它用于描述变形的协调一致性,CC值越高表明数据一致性越强,变形协调性越好,CC=1表明变形完全一致。
1.3 模拟条件和参数
对钛合金通过两相区不同固溶和时效温度及冷却速度控制,可获得不同初生α相含量,次生α片层厚度的组织。目前对于双态组织,采用晶体塑性有限元建模并计算的研究少见,因其构建的几何模型复杂度高,一般Voronoi图法构建的等轴组织无法满足精细描述该组织的要求。对于片层结构,简化的将αs+β假定为一相[7],但是不能反映片层内部的应力应变分布特征;韩逢博[17]采用Python脚本几何建模,获得的片层组织逼近真实组织特征。采用Python方法生成的几何模型,其后续网格划分易出现短边、尖角等,给计算收敛带来困难。作者提出的不重叠控制种子的方法,可减少该问题出现的机率。另外,模型中片层结构包含单变体与实际组织中每个β晶粒中包含多个α变体析出并接触的特征不同。综合上述问题,本文采用INP文件编程并采用规则网格,可规避网格划分的困难并可直接生成目标提交文件,缩短时间流程;另一方面,对片层团簇结构中生成3变体团簇结构(该特征结构实验金相中较常见)以进一步逼近真实钛合金双态组织特征。
图1给出了建立的双态组织2D几何模型。模型基体采用Voronoi图法生成,边界具有周期特征,β母相转变晶粒内包含三种片层集束对应三种变体,变体同母相β之间位向符合Burgers关系,母相β和αp晶体取向随机。整体模型的大小为150×150 μm2,晶粒个数为132=169个,晶粒平均尺寸为13.0 μm,α片层宽度为1 μm。实际组织β片层宽度较小且有一定变化,为便于建模统一将β片层厚度设置为0.5 μm。模型中初始α相含量约为40%,初始α相晶粒和β母相转变晶粒分布混合相对均匀,尽量避免团聚现象。
图1
采用有限元方法结合晶体塑性本构模型,模拟钛合金不同组织高温拉伸变形行为。模拟中的边界条件为:(1)Y=0边,U2=0;(2)X=Y=0原点,U1=0;(3)Y方向Couple上边缘,控制拉伸20%;(4)Y方向两侧面自由边界。模拟时采用Ti-6Al-4V合金,在750℃高温拉伸(忽略在该温度孪生变形,可避免相变和再结晶)。合金在变形中考虑的滑移系列于表1,HCP晶体(α相)同时考虑<a>型滑移系(基面滑移、柱面滑移、锥面滑移)和<c+a>型滑移系(一级和二级锥面滑移);BCC晶体(β相)考虑
表2 Ti-6Al-4V晶体塑性参数(750℃)
Table 2
| Phase | Slip systems type | n | h0 /MPa | τ0 /MPa | τs /MPa |
|---|---|---|---|---|---|
| α-Ti(HCP) | <a> | 6.25 | 120.0 | 8.2 | 18.0 |
| <c+a> | 6.25 | 120.0 | 82.0 | 180.0 | |
| β-Ti(BCC) | 12.5 | 143.1 | 84.3 | 96.5 |
2 模拟结果和讨论
2.1 双态组织变形的应力应变空间分布特征
图2
图2
双态组织的高温拉伸应力应变云图
Fig.2
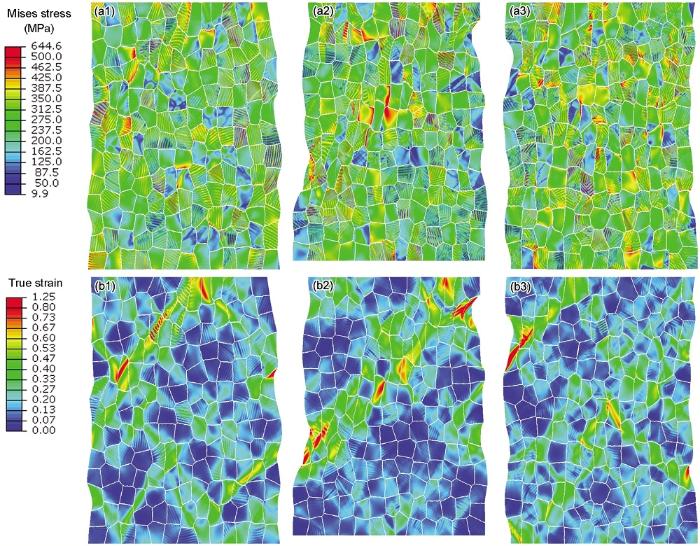
Contour maps of Mises stress and true strain for duplex microstructures (40% αp, 750℃, 20% tension): (a1) (a2) (a3) mises stress, (b1) (b2) (b3) true strain, (a1) (b1) whole, (a2) (b2) αp+αs, (a3) (b3) β phase
从局域空间分布来看,β母相析出的三变体集束变形后应力分布不同,三变体集束应力有高低差异,未见三变体集束同时存在高应力特征,说明高应力集束的产生有近邻片层集束不易变形的诱导作用。高应力变体集束长度方向应力存在梯度变化,有些还处在应力值两级分化的特征。这种类型特征与后续热处理中片层粗化行为可能有关联[39]。
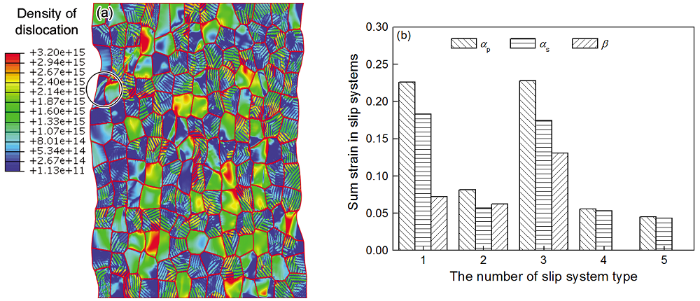
图3a是与图2对应的平均位错密度云图,从图中可见:(1)高位错密度主要存在于αp中,这与图2b1高应变主要存在于αp中特征是一致的,因为高应变一定程度上与高位错密度有关。(2)高位错密度易集中于三叉晶线位置,因为晶内位错滑移易塞积于晶界附近,且三叉晶线处材料性能改变明显,位错滑移协调周围需要的应变量更大。(3)平均位错密度不具有条带特征,因为高应变的位错来源,有些晶粒是平均地激活全部滑移系,这些晶粒同时具有高应变和高平均位错密度;而有些只集中激活部分滑移系(图3a中○区域晶粒),这些晶粒具备高应变和较低的平均位错密度特征,这些晶粒的变形过程开始时部分滑移系率先大量激活,其余部分滑移系部分参与,起协同作用。
图3
图3
双态组织高温拉伸后的平均位错密度云图和各滑移系开动应变统计(40% αp,750℃,20%拉伸)
Fig.3
Contour maps of average dislocation density and statistical true strain of each slip system for duplex microstructures (40% αp, 750℃, 20% tension): (a) average dislocation density, (b) sum true strain of each slip system
图3b给出了20%拉伸后全部晶粒各滑移系累计应变的统计结果,其相应滑移系类型编号见表1。从图中可见:(1)α相部分(αp,αs)<a>型滑移开动应变量明显高于<c+a>,因为<a>型滑移开动临界分切应力和饱和流变应力均明显低于<c+a>型滑移[40]。(2)β相部分
为了定量研究上述多晶变形后应力应变分布情况,提取上述模型中所有单元积分点应力应变值,得到图4给出的应力应变频率统计图。从应力分布角度看(图4a),整体、αp、αs三者的应力频率分布曲线近似正态分布,其峰顶尖锐,其中αp平均应力高于αs;β相的平均应力高于前两者,而其应力分布呈双峰形态,其原因是在多晶非均匀变形中β相应力变化敏感于应变变化,多晶中的晶界易产生高应力集中而晶内的较低,导致双峰形态。从应变分布角度看(图4b),αp应变分布范围宽泛,高应变区间面积大,与前述高应变条带主要来自于αp是一致的;αs和β的应变分布曲线相似度高,说明在变形中两者应变协同一致性强,存在相互激发特征,是两者之间的片层相互交错的结构特征所致。
图4
图4
双态组织的应力应变频率统计图
Fig.4
Frequency of Mises stress and true strain for duplex microstructures (40% αp, 750℃,20% tension) (a) Mises stress, (b) true strain
2.2 初生α相体积分数的影响
图5
图5
初生α相体积分数不同的双态组织的高温拉伸应力应变云图
Fig.5
Contour maps of Mises stress and true strain for alloys different volume fraction of primary α phase(750℃, 20% tension) (a1, a2, a3) Mises stress, (b1, b2, b3) true strain, (a1, b1) 20%, (a2, b2) 40%, (a3, b3) 60%
αp体积分数为20%时αp被片层晶粒包围的结构具有多种特征:(1) αp不完全被包围时不仅需要提供塑性应变,因其含量低为了维持整体的应变量,部分αp在提供高应变的同时还需激活较多相邻αs参与应变。由于(αs+β)存在交错结构进而诱发β相高应变,而β相高应变对应较高应力(如图5a1左○区域αp晶粒激活临近片层的高应力特征);(2) αp晶粒被完全包围时其提供的塑性应变量不充分,与周围(αs+β)结构性能差异大,位错滑移易阻碍于周围界面,并且(αs+β)结构强度高于αp,其“硬相”包围“软相”结构避免了αp高应力的诱发(如图5a1右○区域αp晶粒低应力特征)。另外,因为该组织中的(αs+β)结构晶粒局域团聚几率高,缺乏较软的αp晶粒的应变协调,只能通过充分激发自身内部αs片层应变,进而导致β片层高应力特征(如图5a1□区域晶粒存在此特征)。
为了定量分析钛合金双态组织中的应力应变分布,对其组织模型变形后的相应数据进行分析。统计样本对象包括整体、初生α相(αp)、次生α相(αs)和β相,统计物理参量类型包括Mises应力和真应变,统计数值方法包括平均值和协调系数。于是,通过比对不同样本物理参量平均值的差异获知应力应变的分配特征,通过协调系数高低及变化获知不同组织特征对协调性的影响。
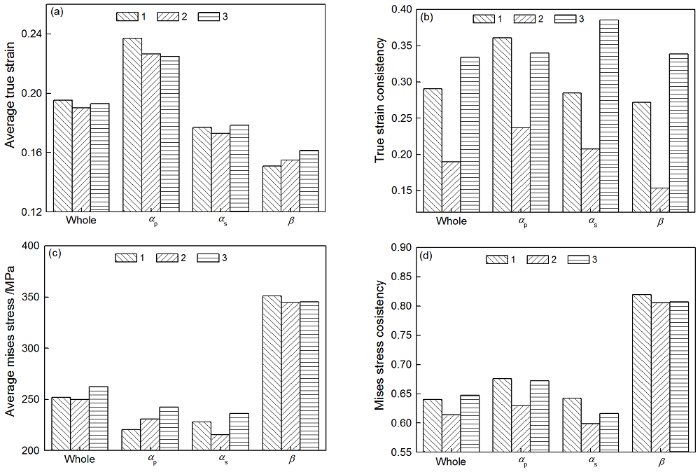
图6给出了不同αp体积分数双态组织高温拉伸20%后各物理量的统计情况。从图6c中整体Mises应力变化可知,对于双态组织,随着αp体积分数的升高强度降低,因为其含量随αp体积分数升高而降低,而β相是强度较高的相。图6a中平均应变大小的排序为:αp>整体>αs>β,即αp在双态组织变形中应变大,是主要应变提供者;αp的平均应变随着αp体积分数的升高而总体略有降低;而αp体积分数10%时应变较低,因为αp体积分数10%时双态组织中αp晶粒几乎被(αs+β)全包围。其全包围结构,一部分取向合适的αp晶粒发生塑性应变,但是高应变被抑制。曲线中αs和β的平均应变曲线形态相似度高,近乎上下平移复制,表明片层结构中αs和β相互协调变形的特征明显,其平均应力曲线同样近乎平移复制(图6c)也表明这一点。从图6c可知,β相在组织中应力高,αp和αs平均应力曲线交缠,表明两者的变形具有塑性应变相互激发特性。
图6
图6
初生α相的含量对双态组织平均应力应变和协调系数的影响
Fig.6
Average Mises stress and true strain, consistency coefficients for duplex microstructures with different volume fraction of primary α (750℃, 20% tension) (a) average true strain, (b) true strain consistency, (c) average Mises stress, (d) Mises stress consistency
从图6b和d可见,随着αp体积分数的升高αp体积分数小于30%时应变协调系数明显降低,αp体积分数大于30%时应变协调系数缓慢降低;αp体积分数大时片层结构被αp包围的几率升高,片层结构较难变形,导致局域αp非均匀应变,故而使整体应变协调性降低;αp体积分数小于30%时应变协调系数明显较低,这与αp被片层不完全包围的结构导致局域变形非协调相关的。整体应力协调系数变化不大。
2.3 α片层厚度的影响
图7给出了不同αs片层厚度组织经750℃高温20%拉伸后的应力应变云图。结果表明,αs片层厚度、长宽比、形态等均可影响材料力学性能[3,6],因为在热处理片层形态控制中αs片层厚度是重要控制指标[41]。为了研究片层形态特征对组织变形行为影响,进行简化几何构型设计,保持αp体积分数40%,改变αs片层厚度,根据实验片层的厚度范围设定设置其厚度。从图7中的几何构型得知,随着αs片层厚度的增大,双态组织多晶体系中αp-αs界面比例在整体中升高,且αp之间αs位错“通道”变宽,而2.2小节中表明αp和αs之间存在塑性应变激发特点,因此该特征影响后续变形。从图7a1、a2、a3中的应力分布可知,局域高应力主要集中于β片层中(图7a1红色特征)。随着αs片层厚度的增大αp晶粒尤其三叉晶线局域高应力比例提高(图7a3红色特征),表明增加片层宽度可释放片层中的高应力。从图7b1、b2、b3中的应变分布可知,依然存在高应变条带特征,高应变集中在αp相晶粒。对比三者应变分布可见,随着αs片层厚度的增大高应变条带的明晰度降低,部分高应变条带退化为断续的孤立区域块。这个结果说明,高应变条带在形成传播中宽αp片层释放周围更多应变,因为αp-αs总界面比例升高,且αp之间αs位错“通道”变宽。这导致αp位错滑移传播进入αs片层可能性和应变量提高,图7b3中○区域αp晶粒和αs片层之间的高应变传播表明了这一点。
图7
图7
具有不同α片层厚度的双态组织的高温拉伸应力应变云图
Fig.7
Contour maps of Mises stress and true strain for microstructures with different α lamella thickness (40% αp, 750℃, 20% tension) (a1, a2, a3) Mises stress, (b1, b2, b3) true strain, (a1, b1) 1.5 μm, (a2, b2) 2.0 μm, (a3, b3) 2.5 μm
图8给出了不同α片层厚度条件下双态组织平均应力应变和协调系数变化曲线图。从图8c中整体平均Mises应力的变化可知,对于双态组织,随着αs片层厚度的增大合金强度略微降低,这是基于组织中αs片层厚度的增大β相体积分数略微减少所致。图8a、c、d表明,各统计对象平均应力应变和应力协调性数值变化较小,αp晶粒保持平均应变较大的特征(图8a),是高应变分配对象。αp晶粒和αs片层平均应变曲线收敛于整体平均应变曲线,表明两种应变交互作用增强,与其应变分布云图分析的特征是一致的。从图8b可知,随着αs片层的增厚整体、αp、αs和β的应变协调性都总体升高,是厚αs片层部分释放αp高应变的结果;特别是片层厚度2.5 μm时αs其应变协调性甚至高于αp,说明高应变的充分释放减小了应变分布的差异性。综合钛合金双态组织αs片层厚度增加对高温拉伸变形行为影响,整体平均应力应变变化不大,而应变协调系数升高。结合协调系数公式(5)定义,表明合金的失效可能性降低,与实验中断裂韧性的提高是一致的[4]。
图8
图8
α片层厚度对双态组织平均应力应变和协调系数的影响
Fig.8
Average Mises stress and true strain, consistency coefficients for duplex microstructures with different α lamella thickness (40% αp, 750℃, 20% tension) (a) average true strain, (b) true strain consistency, (c) average Mises stress, (d) Mises stress consistency
2.4 α片层变体团簇数目的影响
为了便于讨论αs片层变体类型数目对双态组织高温拉伸变形行为影响,设定相同的αs片层厚度2.0 μm,变体类型数目分别为3、2和1,并统一从界面向中心延伸交叉。对比图9中几何形态特征,变体数目的减少,一方面导致β转变组织内形态复杂度降低,片层间性质一致性增强,特别是单变体片层团簇避免了不同变体片层的交互作用;但是,另一方面β转变组织内αs片层同周围晶粒可供协调滑移的种类减少。这两方面对整体变形协调的影响具有相反的特征,影响变形后的应力应变分布差异。
图9
图9
具有不同α片层团簇数目的双态组织高温拉伸应力应变云图
Fig.9
Contour maps of Mises stress and true strain in microstructures with different numbers of α lamella colony (40% αp, 750℃, 20% tension) (a1, a2, a3) Mises stress, (b1, b2, b3) true strain, (a1, b1) 1, (a2, b2) 2, (a3, b3) 3
图10给出了不同α片层团簇数目对双态组织平均应力应变和协调系数的影响统计图。从图10c中整体平均Mises应力变化可知,αs片层变体数量改变,对其强度影响不大,因为组织α片层团簇数目改变对β体积分数几乎没有影响。从图10a、c、d可见,随着变体数目的减少相应的各统计对象平均应变变化较小;2变体片层结构的整体应力和应力协调系数略微低于其他两种,其变化幅度明显低于αp体积分数和αs片层厚度改变对合金的影响。图10b中的2变体片层结构,变形后的应变协调性明显低于其它两种。图10b中2变体片层结构,其应变协调性明显低于其它两种。其原因是,假定同一母相β中12变体等机率出现,根据β和α之间满足Burgers关系所对应的α/α不同变体取向差统计结果[45,46],计算出2变体出现小角晶界的机率为p2=14/144≈9.72%,相应3变体存在小角晶界机率为
图10
图10
α片层团簇数目对双态组织平均应力应变和协调系数的影响
Fig.10
Average true strain and Mises stress, consistency coefficients for microstructures with different numbers of α lamella colony (40% αp, 750℃, 20% tension) (a) average true strain, (b) true strain consistency, (c) average Mises stress, (d) Mises stress consistency
综合上述双态组织钛合金高温变形模拟研究结果,双态组织高温变形中αp是高应变分配对象。随着变形量的增大各晶体应变激活具有层级特征,αp晶粒应变优先激活,进而激活的是优先变形的αp晶粒近邻的同属性αs片层应变,因为αs和β片层相互交错最后激活“硬相”β片层。三个层级晶粒塑性流动性和强度依次变化,从而使双态组织同其它组织相比,综合性能较为优异。考虑到Hall-Petch效应和晶体取向特征,更详细的应变激活优先级排序为:αp>粗αs片层>细αs片层>β片层>基面织构αp片层。该优先级对象的塑性流动性依次降低,强度依次升高。其中β片层具有较高强度和充足滑移系,一方面可缓解高应力集中,另一方面可化解裂纹进一步扩展及增加裂纹扩展路径。基面织构αs片层作为最强硬化相,应避免过多富集(微织构),使周围结构不足以补充协调其局域应变,从而导致裂纹易于生成和扩展。
根据双态组织中各相力学特性,本文提出一些组织设计建议。对于αp尺寸和比例的控制,αp比例应调控适中。αp比例较高则其塑性好但协调性较低,未能充分调动激活片层结构来提供强度;αp比例低于20%时αp多被“硬化”片层结构包围,其塑性功能未能充分激活,合金强度较高,而塑性降低。对于αs片层的调控,应包含多变体,片层宽度具有一定范围,从而使αs应变充分激活,具有依次递增层级特征。结合Hall-Petch效应和多界面阻碍裂纹扩展作用,单一化变体种类且过薄αs片层(相对αp尺寸)应避免。
3 结论
(1) 在Ti-6Al-4V双态组织高温变形中αp是高应变分配相,变形后出现高应变交叉条带并近似对称于拉伸方向。αp和αs应力应变频率统计均呈现单峰形态,而β相应力呈现双峰形态。
(2) 双态组织中的αp与αs应变协调关联性强,αp与βT之间的包围结构特征加剧局域应变差异。随着合金αp相体积分数的提高αp晶粒平均应变分配降低,整体应变协调性先较快降低而后平稳。
(3) 双态组织αs片层厚度的增大使其高温变形后高应变条带特征弱化,整体应变协调系数升高。改变β转变组织中αs的变体数量其应力协调系数变化不大,β母相中包含两种变体片层团簇,其应变协调性比单变体和三变体结构的低。