冷拉拔钢丝横截面应变不均匀性的晶体塑性研究

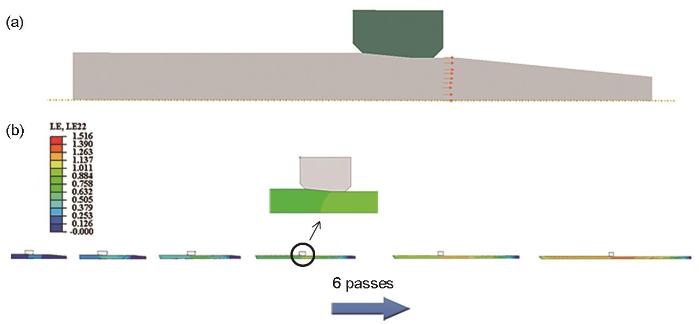
图1 拉拔的二维轴对称模型

Fig.1 A two-dimensional axisymmetric model for drawing (a) initial state, (b) deformation process of steel wire

钢丝连续拉拔仿真模型使用Abaqus/Standard求解器，采用四边形网格即CAX4R，钢丝包含14358个单元，模具包含808个单元。模型的计算结果用于分析钢丝在典型拉拔工艺下的应力应变分布规律，并为后续晶体塑性模型提供边界条件。

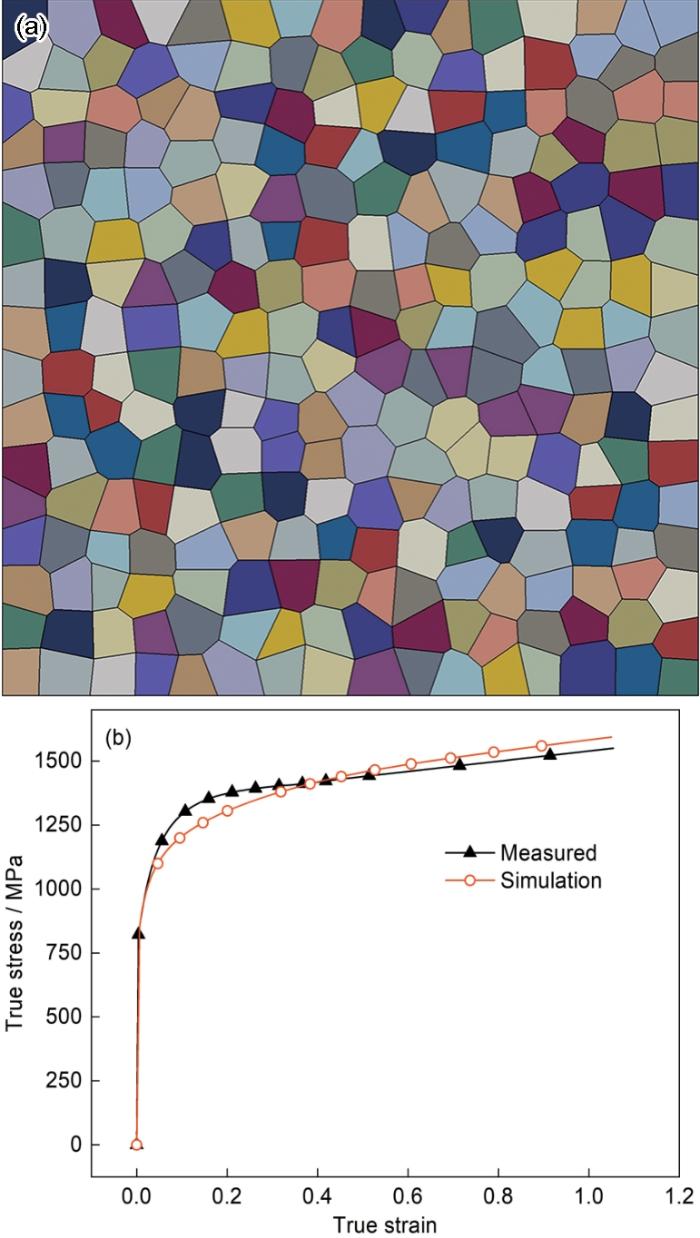
文中仿真所用的材料参数用实验获得。从盘条上截取样本制备了直径为8 mm长度为12 mm的圆柱试样，按国家标准GB/T 7314-2017在TSE 105D微机控制电子万能试验机上进行室温下单轴压缩实验，得到压缩变形时珠光体盘条的工程应力-工程应变曲线。但是，试样端面受到的压缩模具的摩擦约束使其在压缩过程中出现非均匀鼓胀变形，不能直接用简单公式计算真应力-真应变曲线。因此文中采用材料参数反求计算方法，通过对比仿真和实验的盘条压缩工程应力-工程应变曲线迭代更新待求的真应力-真应变曲线，直至仿真曲线与实验曲线吻合良好(图2a)，从而得到较准确的真应力-真应变曲线。最后，基于线性强化法则^[5,20]，将应力应变曲线线性外延求得钢丝塑性变形后期无法用实验得到的数据，如图2b所示。

图2

图2 反求法中吻合良好的工程应力-工程应变曲线和仿真模拟使用的材料真应力-真应变曲线

Fig.2 Engineering stress-strain curves with good agreement through the reverse method (a), and true stress-strain curve of the material used for simulation (b)

1.2 晶体塑性模型

鉴于珠光体钢丝的冷拉拔塑性变形主要发生在珠光体铁素体中，且珠光体铁素体的主要塑性变形机制为位错滑移，文中采用基于位错密度的晶体塑性本构研究细观尺度上材料变形行为，其基本原理和方程与文献[22]的相同：在连续介质力学中，质点的总变形梯度可分解为弹性变形梯度 F^e 和塑性变形梯度 F^p，前者表示晶格的拉伸和刚性旋转，后者表示滑移系上的塑性剪切：

F = F^{e} F^{p}

(1)

塑性变形梯度 F^p的演化可由塑性变形速度梯度 L_p 表示：

\dot{F_{p}} = L_{p} F_{p}

(2)

塑性变形速度梯度 L_p 可通过所有滑移系上塑性滑移量的总和

L_{P} = \sum_{α}^{n s s} {\dot{γ}}^{(α)} s^{(α)} \otimes n^{(α)}

(3)

计算。其中 $\dot{γ}$ ⁽^α⁾为滑移速率，s⁽^α⁾和n⁽^α⁾分别表示α滑移系的滑移方向和滑移面法向的单位向量，nss为滑移系个数。 $\dot{γ}$ ⁽^α⁾又可表达为一系列内部状态变量的函数，根据率相关晶体塑性本构，α滑移系上的剪切速率 $\dot{γ}$ ⁽^α⁾演化遵循

{\dot{γ}}^{(α)} = {\dot{γ}}_{r e f}^{(α)} {|\frac{τ^{(α)}}{τ_{r e f}^{(α)}}|}^{n} s i g n (τ^{(α)})

(4)

其中 ${\dot{γ}}_{r e f}^{(α)}$ 为常数，n为这种材料的速率敏感指数。仅当分切应力 $τ$ ⁽^α⁾超过临界分切应力 $τ_{r e f}^{(α)}$ 时α滑移系才能够明显开动，二者可分别表示为

τ^{(α)} = s_{i}^{(α)} σ_{i j} n_{j}^{(α)}

(5)

τ_{r e f}^{(α)} = τ_{y}^{(α)} + G \sum_{β}^{n s s} b \sqrt[]{a_{α β} ρ_{i m}^{(β)}}

(6)

式(5)中的 σ_ij 为柯西应力张量，模型所用柯西应力率为

σ_{i j}^{∆} = C_{i j k l} (D_{k l} - D_{k l}^{p}) - W_{i k}^{p} σ_{k j} - W_{j k}^{p} σ_{k i}

(7)

其中 D 为拉伸张量， W 为反对称自旋张量，上标p为其塑性部分。 C_ijkl 为弹性系数，对于立方晶系由三个独立的弹性常数C₁₁、C₁₂、C₄₄决定。式(6)中的 $τ_{y}^{(α)}$ 为滑移系α的静态屈服应力，G为材料的剪切模量，b为柏氏矢量。第二项表示滑移系之间的交互作用所造成的强化，与相互作用系数a_αβ 和滑移系β上的不可动位错密度 $ρ_{i m}^{(β)}$ 有关，于是在本构关系中引入了位错密度。

位错是珠光体铁素体塑性变形的载体，位错增殖是其强化的主要方式。为了更准确地计算材料的塑性变形，需使用计及位错的本构方程，以合理体现位错的产生和湮灭对位错密度的影响及其对临界分切应力的影响。因此，将位错密度作为晶体塑性本构模型的内在变量，把总位错密度分为可动位错密度(ρ_m)和不可动位错密度(ρ_im)两部分。随着滑移系上应变量的增大，位错密度随之提高。同时，不可动位错阻碍可动位错的运动，而部分可动位错又会转化为不可动位错。滑移系上位错密度的演化可表示为

\frac{d ρ_{m}^{(α)}}{d t} = |{\dot{γ}}^{(α)}| (\frac{g_{s o u r}}{b^{2}} (\frac{ρ_{i m}^{(α)}}{ρ_{m}^{(α)}}) - g_{m i n t e r} ρ_{m}^{(α)} - \frac{g_{i m m o b}}{b} \sqrt[]{ρ_{i m}^{(α)}})

(8)

\frac{d ρ_{i m}^{(α)}}{d t} = |{\dot{γ}}^{(α)}| (g_{m i n t e r} ρ_{m}^{(α)} + \frac{g_{i m m o b}}{b} \sqrt[]{ρ_{i m}^{(α)}} - g_{r e c o v} ρ_{i m}^{(α)})

(9)

式中g_sour为位错源引发的使可动位错密度提高的新的位错，g_minter为林位错相互作用、障碍物周围的交滑移以及位错间交互作用引起的可动位错密度的降低，g_immob为可动位错固定成为不可动位错，g_recov为不可动位错重排和湮灭。

将上述原理写入Abaqus的用户材料子程序(UMAT)，从而实现在Abaqus中的计算。

1.3 多晶珠光体团简化模型和晶体塑性模拟参数

珠光体中的铁素体片层与渗碳体片层相互交叠。渗碳体作为具有复杂晶格结构的硬脆相，其强度高且塑性变形能力有限。相关研究表明，在拉拔应变量小于2时塑性变形主要发生在铁素体内^[23]。在变形过程中铁素体内的位错大量增殖并缠结，产生十分显著的加工硬化效应，是本文的主要分析对象。因此，为了简化计算本文的晶体塑性模型，将珠光体视作一个整体赋予等效材料参数，即在模型中用具有等效参数的等轴晶代表初始盘条中的珠光体团，避开了纳米尺度铁素体和渗碳体片层的处理^[4,5]。根据铁素体滑移系特征设置等效模型中的滑移系，并考虑到铁素体bcc结构具有48个可能的滑移系。但是，拉拔过程温度较低，其他滑移系不易开动^[24~27]。因此，为了简便模型只考虑最易开动的{110}<111>12个滑移系。

按照上述思路，使用Abaqus软件建立了简化的珠光体团代表性体积单元(RVE)模型，如图3a所示。综合考虑计算效率和准确性，将模型边长设置为200 μm，总晶粒数量为256个，珠光体团平均尺寸为12.5 μm，与扫描电镜表征的初始盘条中珠光体团尺寸一致。这种设定，在兼顾计算效率的同时，既能有效减少边界效应的影响也为后续分析提供了足够的统计基数。模型中的每一等轴晶粒代表一个珠光体团，其初始取向为随机生成，各晶粒除晶体学取向不同外，其他材料参数相同。

图3

图3 二维珠光体团RVE模型以及实验和模拟的真应力-真应变曲线

Fig.3 2D pearlite colony RVE model (a) and experimental and simulated true stress-strain curves (b)

为了得到晶体塑性模拟的材料参数，在Abaqus中对代表性体积单元模型施加压缩载荷，对比前文单轴压缩实验获得的真应力-真应变曲线拟合出晶体塑性模型所需的材料参数，根据模拟对象特征参考相关文献确定其中的柏氏矢量、速率敏感指数、滑移系静态屈服应力。拟合得到的参数列于表2，其中ρ_im0和ρ_m0为不可动位错和可动位错的初始密度，a_αα为滑移系的自硬化系数， $\dot{a}$ 为模型的参考应变速率，压缩模型中的 $\dot{a}$ 按实际情况设为8.74 × 10^-4 s^-1。在拉拔模型中，以最终出口速度为1 m/s估算， $\dot{a}$ 取各道次的应变速率平均值30 s^-1。从图3b可以看出，模拟结果与实验结果在弹性段与塑性段均吻合较好。因此可以认为，拟合得到的材料参数能准确地反映珠光体团的塑性变形行为。

表2 计算等效珠光体材料的晶体塑性需要的参数

Table 2 Parameters required for crystal plasticity calculation of equivalent pearlite material

Parameter	Symbol	Value
Elastic moduli	C₁₁	197000 MPa
	C₁₂	134000 MPa
	C₄₄	105000 MPa
Rate sensitivity parameter	n	10 ^[27]
Reference strain rate	$\dot{a}$	8.74 × 10^-4 s^-1
Burgers vector	b	2.48 × 10^-7 mm ^[28,29]
Dislocation density	g_minter	0.6
evolution coefficient	g_immob	0.035
	g_recov	80
	g_sour	10^-5
Initial dislocation density	ρ_im0	240000 mm^-2
	ρ_m0	240000 mm^-2
Static yield stress	τ_y	120 MPa ^[30,31]
Shear moduli	G	115022 MPa
Interaction coefficient	a_αα	0.8
	a_αβ	0.6

新窗口打开| 下载CSV

采用Abaqus子模型功能将晶体塑性RVE模型与宏观有限元模型耦合，选取盘条横截面上不同位置的微区，将宏观模型中微区边界节点的位移通过插值赋予RVE模型，从而为RVE模型提供对应的边界条件。与以往一些做法^[32,33]中的“对称+单轴拉伸”边界条件不同，这种做法能更好地将宏观拉拔变形的微区变形特征引入晶体塑性RVE模型。

2 模拟结果

2.1 钢丝横截面应变的分布和路径

钢丝的拉拔应变量可表示为ε = 2ln(d₀/d)，其中d₀为钢丝初始直径，d为拉拔后钢丝直径。但是，在拉拔过程中钢丝的实际受力和变形较为复杂，其横截面上的应变分布并不均匀。图4a给出了钢丝横截面上应变分布的计算结果。可以看出，无论是轴向应变还是径向应变其分布均呈现出从钢丝心部到表面先升高再降低的特征，次表层的应变最大。图4b给出了钢丝横截面上等效应变的计算结果，也呈现出从心部到表面先升高再降低的分布特征。在拉拔过程中轴向的牵拉与模具的挤压和摩擦，是产生这种应变分布特征的关键因素^[10]。

图4

图4 拉拔后钢丝横截面上轴向和径向应变的分布以及等效应变分布和RVE模型计算选点

Fig.4 Distribution of axial and radial strains on the cross-section of steel wire after drawing (a) and distribution of equivalent strain on the cross-section of steel wire after drawing and selection of microscopic model calculation points (b)

由于钢丝横截面不同位置的受力状况不同，横截面上除应变的不均匀分布外，不同位置的应变路径也显著不同。应变路径，是一个描述加工历史的概念。在一般情况下，应变张量[ε_ij ]有9个非零分量，其中5个是独立的，即有5个自由度。因此，每一个应变状态对应五维空间中的一个点，随着加工过程的进行该点的位置不断变动，其在五维坐标系中运动的轨迹即为应变路径^[9]。由Schmitt^[34]引入的SF因子

S F = \frac{[ε] : [ε']}{{([ε] : [ε])}^{\frac{1}{2}} \cdot {([ε'] : [ε'])}^{\frac{1}{2}}}

(10)

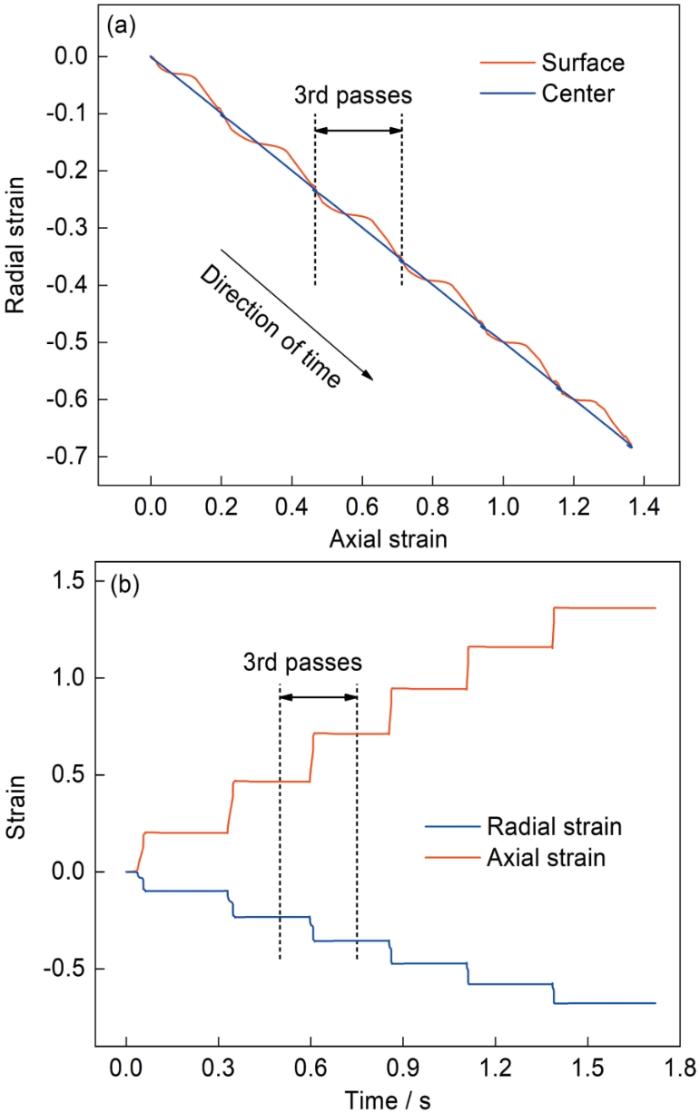
是表示应变路径的定量指标，其物理意义是应变空间中相邻时间段塑性应变张量[ε]和[ε′]之间夹角的余弦。在本文的研究中，由于拉拔变形的轴对称特征部分切应变分量为零，且拉拔轴方向(轴向)和钢丝半径方向(径向)是重点关注的方向。因此，本文采用简化的应变路径表示方法，如图5a所示，将轴向应变与径向应变的散点图按拉拔时间顺序连接形成了应变路径图，比SF因子表示法更加直观。

图5

图5 拉拔模拟所得钢丝表面和心部的应变路径图及钢丝表面轴向和径向应变随时间变化曲线

Fig.5 Strain path diagrams of surface and center in steel wire obtained from drawing simulation (a) and time dependent curves of axial and radial strain of surface in steel wire obtained from drawing simulation (b)

为了更清晰地解释应变路径的含义，图5b给出了轴向应变和径向应变随时间的变化。在本文的拉拔模型中，各道次的时长均约为0.25 s。但是，对于一个固定的物质点，其经历塑性变形的时间很短，在模型的不同道次中变形时间为0.003~0.02 s，因此图5b中的曲线呈现出台阶状。图5b中的一条水平线段表示应变保持不变，对应图5a中的一个点，而图5b中的台阶对应短时间内应变迅速增大的过程。图5a能体现这一过程的更多细节，例如两个方向上变形的比例关系和先后顺序。由此可见，应变路径图比应变随时间的变化能呈现出更多的信息。

在钢丝横截面的不同位置，即使最终的总应变相同材料变形所经历的应变路径也不同。如图5a所示，钢丝心部变形经历的应变路径较为简单，可认为是等比例加载，其变形各个时刻的SF均为1；而靠近表面区域的应变路径则比较曲折，Δε_r/Δε_a不断变动(ε_r表示径向应变，ε_a表示轴向应变)。在每道次拉拔过程中，先发生一定的轴向与径向协同变形，然后变形方向明显变化而转变为以轴向应变为主，随后又转变为两向应变同时发生。进一步地，对横截面不同位置处应变路径的观察表明，应变路径的曲折程度与该位置到钢丝心部的距离正相关。

在冷拉拔过程中横截面各处的应变量和应变路径的差异对材料的微区力学行为的影响，可能导致钢丝不同位置的显微组织演化不同，并最终造成硬度的不均匀分布。

2.2 微区力学响应和硬化行为

选取图4b等效应变 $\bar{ε}$ 分布曲线中的6个点O、A、B、C、D、E，以子模型方式将各点的变形特征导入RVE模型，观察其力学响应的差异。其中点O、A、B、C的等效应变量依次升高，点E、D的应变量分别与点A、B相同，但是应变路径更曲折复杂。

拉拔结束后提取钢丝横截面上6个RVE模型中滑移系的总剪切应变和不可动位错密度的平均值，用以衡量材料加工硬化程度，如图6所示。根据晶体塑性理论，若滑移系上的分切应力超过其临界分切应力则滑移系开动，且随着滑移应变的增大位错相互缠结固定而产生位错强化。因此，在其他条件相同的条件下，滑移系上总剪切应变越大，不可动位错密度越高，硬化越显著，则材料硬度就越高。观察发现，O、A、B、C 4点的滑移系总剪切应变和不可动位错密度总体上都呈上升趋势，表明微区强化程度与等效应变量呈正相关。需要注意的是，观察A-E、B-D两对点发现，在等效应变量相同的情况下，靠近钢丝表面的点处滑移系的总剪切应变和不可动位错密度更高，意味着曲折多变的应变路径能产生更强的强化效应。模拟结果表明，综合应变量和应变路径的影响使位于次表层的D点处硬化程度最高。这个结果与文献^[9,35]中关于钢丝次表层硬度高于心部的结论一致。

图6

图6 6个代表点处RVE模型中滑移系总剪切应变和不可动位错密度两个指标的平均值

Fig.6 Average of two values in RVE of six positions at end time of drawing (a) total cumulative shear strain (γ) on all slip systems, (b) total density of immobile dislocation (IMDD) on all slip systems

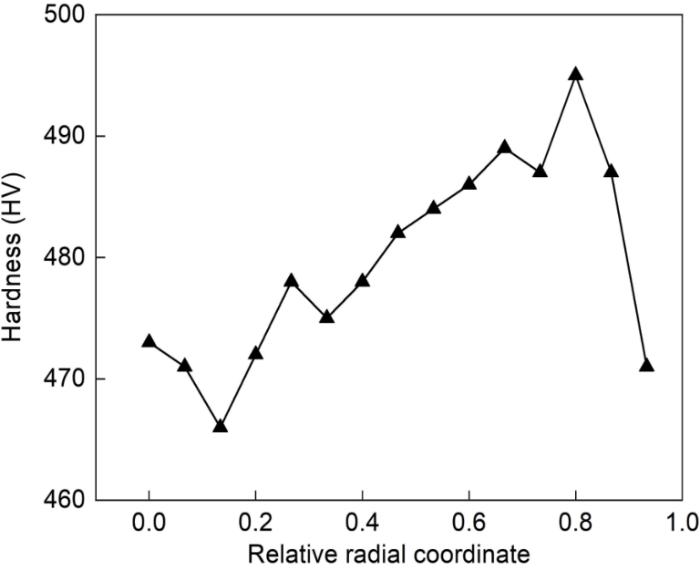
为了验证模拟结果，测量了相同拉拔工艺的钢丝横截面上不同位置的维氏硬度，结果如图7所示。可以看出，钢丝横截面的硬度从心部到表面整体上呈现先升高后降低的变化趋势，且次表层硬度最高。这个结果，与模拟得到的规律相同。但是，盘条横截面上的化学成分和初始组织的不均匀性，使实验测得的硬度曲线出现一定的波动，其变化规律与模拟结果不能完全准确对应。

图7

图7 钢丝横截面上维氏硬度的测量结果

Fig.7 Measurement results of Vickers hardness on the cross-section of steel wire

3 讨论

钢丝横截面近表面区域的应变路径曲折复杂，Δε_r/Δε_a比较多变。这是多变的应力状态决定的。模具摩擦力的影响，使该区域受到的切应力显著大于心部，且钢丝表面与模具锥角的适配形成的切应变加剧了应力应变演变的复杂性。因此，E、D两点的较大且不断变化的切应力一方面使其Mises等效应力增大，另一方面使其主应力的方向不断变化。在更高的Mises应力和主应力方向不断变动的作用下，分配到某滑移系上的分切应力可能达到更高的数值，从而诱发滑移系的开动。

图8a以A点为例给出了拉拔过程中RVE上平均Mises等效应力的变化，曲线上的尖峰代表该点正在经过拉拔模具进行变形。以第1道次的Mises应力峰值为例，对比6个点处的应力峰值，如图8b所示。在A-E、B-D两对等效应变相同但应变路径不同的点中，E、D两点的峰值Mises应力分别高于A、B两点，表明复杂应变路径下材料的Mises应力更高。

图8

图8 A微区平均Mises等效应力随时间变化图和第1道次中各点Mises等效应力峰值对比图

Fig.8 Average von Mises stress over time in micro zone A (a) and comparison of peak von Mises stress at various points in the first pass (b)

更高的应力水平，可能驱动更多的滑移系开动。以第1道次末滑移系开动数目为分析对象，提取了A、B、D、E 4个点处RVE模型上的滑移系开动数目分布，如图9所示。A点RVE模型中滑移系开动数目集中在8~10个，而对应的E点RVE模型中滑移系开动数目集中在10~12个。类似地，应变路径简单的B点RVE模型中，滑移系开动数≥ 11个的比例约为35%，而等效应变相同但是应变路径复杂的D点RVE模型中的滑移系开动数≥ 11个的比例约为65%。这表明，在等效应变大小相同的情况下，复杂的应变路径能使更多的滑移系开动。

图9

图9 4个点对应的RVE模型在1道次末的滑移系开动情况分布

Fig.9 Distribution of slip system motion at end of first pass for RVE model corresponding to four points (a) points A and E, (b) points B and D

由于各晶粒的初始取向不同，滑移系的开动情况也不同。因此，上述从统计角度分析RVE中所有积分点滑移系开动情况后，为了进一步分析复杂应变路径诱导额外强化的机理，在RVE模型中远离边界的中心部位随机选取一个代表性晶粒，如图10所示，进一步对比A、E两点微观响应的差异。选取的晶粒初始取向为：[54 $\bar{2}$ ]晶向平行于钢丝径向，[10 $\bar{1}$ 23]晶向平行于拉拔轴向，[2 $\bar{3}$ $\bar{1}$ ]方向平行于钢丝周向。

图10

图10 选取典型晶粒的示意图

Fig.10 Schematic diagram of selecting typical grain

提取该晶粒上各积分点的滑移系开动数目，列于表3。可以看出，A点有近一半的积分点开动了9个滑移系，而E点则大多开动了11个滑移系。图11a、b给出了该晶粒上12个滑移系的总剪切应变云图，可见E点处典型晶粒中不仅开动的滑移系数目更多而且总滑移应变更大。这表明，近表面区域主应力方向的不断变动使各个取向的滑移系开动的几率更高。同时，随着总剪切应变的增大可移动位错不断缠结和钉扎，使不可移动位错的密度提高。如图11c、d所示，E点处的典型晶粒中不可动位错的密度明显高于A点处对应晶粒中的不可动位错密度。这些规律，与图6给出的RVE模型整体层面上的规律是一致的。滑移系的临界分切应力可代表其强度，提取了A、E两点RVE模型中典型晶粒上的12个滑移系的平均强度变化曲线，如图12所示。可以看出，E点的强度更高。其原因是其不可动位错密度更高，位错强化作用更强，从而提高了各滑移系的临界分切应力，最终使E点的微区硬度高于A点。

表3 A、E两模型中代表性晶粒上的滑移系开动数目分布

Table 3 Distribution of numbers of activated slip systems on representative grains in models A and E

Number	Model A	Model E
8	28%	0
9	44%	0
10	16%	22%
11	4%	61%
12	9%	16%

新窗口打开| 下载CSV

图11

图11 第一道次末代表性晶粒上的微观响应

Fig.11 Microscopic response on representative grains at the end of the first pass (a) total cumulative shear strain at point A, (b) total cumulative shear strain at point E, (c) total density of immobile dislocation at point A, and (d) total density of immobile dislocation at point E

图12

图12 A、E两点在代表性晶粒上的各滑移系平均强度随各道次进行的变化

Fig.12 Variation of average strength of slip systems on representative grains at points A and E

上述分析表明，在相同应变下曲折应变路径引起了额外的强化，是除横截面应变不均匀外引发冷拔钢丝横截面上硬度不均匀的另一个重要机制。

4 结论

(1) 将宏观有限元与晶体塑性有限元相结合研究发现，冷拉拔后钢丝横截面上塑性应变呈现从心部到表面先升高再降低的分布特征，次表层塑性应变最大；钢丝心部变形经历的路径可认为是等比例加载，而靠近表面区域的应变路径比较曲折。

(2) 钢丝横截面上的应变路径差别不大时，微区应变量越大则加工硬化越剧烈；在应变量相同而应变路径不同时，应变路径越曲折则加工硬化越剧烈。两种效应的结果是，在冷拔钢丝横截面上近表面区域硬度最高。

(3) 曲折多变的应变路径产生额外强化的原因是，复杂的应力状态开动了更多的滑移系进而使滑移应变增大和不可动位错密度提高，最终提高了钢丝的硬度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Y Y

The microstructure and mechanical performance of high speed severe cold drawn steel wire

[D]. Nanjing: Southeast University, 2006

涂益友

高速大应变冷拔钢丝的组织和力学性能

[D]. 南京: 东南大学, 2006

[2]

M G

Influence of drawing process and die on mechanical properties of steel wire

[D]. Guiyang: Guizhou University, 2006

马明刚

拉拔工艺及模具对钢丝力学性能的影响

[D]. 贵阳: 贵州大学, 2006

[3]

Nam

W J

, Bae

C M

Void initiation and microstructural changes during wire drawing of pearlitic steels

[J]. Mater. Sci. Eng., 1995, 203A(1-2) : 278

[4]

Borchers

, Kirchheim

Cold-drawn pearlitic steel wires

[J]. Prog. Mater. Sci., 2016, 82: 405

DOI URL [本文引用: 3]

[5]

, Bao

S Q

, Zhao

, et al.

Evolution of microstructure and properties for high carbon steel wire during drawing

[J]. J. Mater. Sci. Eng., 2021, 39(6): 937

瞿熙, 鲍思前, 赵刚等.

高碳钢丝拉拔过程中的组织性能演变

[J]. 材料科学与工程学报, 2021, 39(6): 937

[6]

Zhang

X D

, Godfrey

, Huang

X X

, et al.

Microstructure and strengthening mechanisms in cold-drawn pearlitic steel wire

[J]. Acta Mater., 2011, 59(9): 3422

[7]

Liu

Y D

, Jiang

Q W

, Zhao

, et al.

Texture analysis and simulation of pearltic wires during drawing

[J]. Acta Metall. Sin., 2002, 38(11): 1215

刘沿东, 蒋奇武, 赵骧等.

拉拔过程中珠光体钢丝帘线的织构分析与模拟

[J]. 金属学报, 2002, 38(11): 1215

应用精确的线材织构测量方法,对珠光体钢丝帘线的织构进行了测量,实验结果表明,拉拔角、钢丝帘线与拉拔模具间的摩擦力是影响织构形成的主要因素大的拉拔角,会导致在表层或亚表层形成{110}环状织构,从而降低其拉拔及扭转能力.应用Taylor模型可以很好的对这一现象进行解释.

[8]

Zhang

X D

, Godfrey

, Liu

, et al.

Evolutions of microstructure and ferritic micro-orientation and texture in a pearlitic steel wire during cold drawing

[J]. Acta Metall. Sin., 2010, 46(2): 141

张晓丹, Godfrey

, 刘伟等.

珠光体钢丝冷拉拔过程中微观组织及铁素体微区取向与织构演变

[J]. 金属学报, 2010, 46(2):141

DOI [本文引用: 1]

采用电子通道衬度(ECC)和电子背散射衍射(EBSD)技术研究了珠光体钢丝冷拉拔过程中微观组织的变化、铁素体微区取向与织构演变. 结果表明, 珠光体变形组织中存在剪切带(S带),它们的出现与渗碳体片条和拉拔方向之间的夹角有关: 夹角越大, S带越多.随着拉拔应变量的增大, 纵截面上珠光体片条逐渐转向拉拔方向, S带方向与拉拔方向的夹角逐渐减小. 珠光体内的S带会引起铁素体晶粒局部微区取向急剧变化, 从而使原有的珠光体团分裂成若干个由铁素体大角度晶界相隔的区域. 钢丝拉拔过程中形成平行于拉拔方向的铁素体丝织构, 随着应变量的增大, 平行于拉拔方向的铁素体丝织构增强, 其它丝织构组分减弱; 靠近钢丝中心区域内的丝织构增强幅度大于其它区域.

[9]

Zhao

T Z

Strain path effects on the pearlitic steel wire during cold drawing

[D]. Beijing: University of Chinese Academy of Sciences, 2014

赵天章

珠光体钢丝冷拉拔过程中应变路径效应的研究

[D]. 北京: 中国科学院大学, 2014

[10]

Celentano

D J

, Palacios

M A

, Rojas

E L

, et al.

Simulation and experimental validation of multiple-step wire drawing processes

[J]. Finite Elem. Anal. Des., 2009, 45(3): 163

DOI URL [本文引用: 2]

[11]

Toribio

, Lorenzo

, Vergara

On the use of varying die angle for improving the resistance to hydrogen embrittlement of cold drawn prestressing steel wires

[J]. Eng. Fail. Anal., 2015, 47: 273

[12]

Hwang

J K

, Yi

I C

, Son

I H

, et al.

Microstructural evolution and deformation behavior of twinning-induced plasticity (TWIP) steel during wire drawing

[J]. Mat. Sci. Eng., 2015, 644A: 41

[13]

Yang

Z J

, Wang

K K

, Yang

Optimization of steel wire drawing process based on deform and response surface methodology

[J]. J. Nets. Form. Eng., 2019, 11(2): 9

杨祖建, 王开坤, 杨艳.

基于Deform和响应曲面法的钢丝拉拔工艺优化

[J]. 精密成形工程, 2019, 11(2): 9

[14]

Zhao

T Z

, Zhang

S H

, Zhang

L Y

, et al.

Numerical simulation on influence of residual stress on strength gradient in cold drawn steel wire

[J]. J. Plast. Eng., 2016, 23(5): 96

赵天章, 张士宏, 张凌云等.

残余应力影响冷拉拔钢丝强度梯度的数值仿真

[J]. 塑性工程学报, 2016, 23(5): 96

[15]

Roters

, Eisenlohr

, Hantcherli

, et al.

Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: theory, experiments, applications

[J]. Acta Mater., 2010, 58(4): 1152

[16]

Jia

C N

Mesoscopic modeling and simulation of microstructural evolution in Fe-C-Mn steels

[D]. Hefei: University of Science and Technology of China, 2022

贾春妮

Fe-C-Mn合金微观组织行为的介观尺度建模与模拟

[D]. 合肥: 中国科学技术大学, 2022

[17]

, Wang

Z X

, Wang

F Z

, et al.

Progress of microstructure evolution simulation in metal rolling process with plastic finite element method

[J]. Mater. Rep., 2013, 27A(2) : 138

陆璐, 王照旭, 王辅忠等.

塑性有限元法在金属轧制过程中组织演化模拟进展

[J]. 材料导报, 2013, 27A(2) : 138

[18]

Ling

B C

Simulation analysis on damage process and torsional performance improvement of ultra-high strength steel wire drawing process

[D]. Nanjing: Southeast University, 2017

凌必超

超高强度钢丝拉拔损伤过程模拟分析及扭转性能提升

[D]. 南京: 东南大学, 2017

[19]

Wang

, Chen

, Li

Z X

, et al.

Modeling of wire with flaw in multi-drawing and optimization of drawing technique

[J]. Mech. Eng., 2009, 31(1): 28

王珺, 陈翠, 李兆霞等.

含缺陷钢丝多道次拉拔模拟及工艺参数优化

[J]. 力学与实践, 2009, 31(1): 28

[20]

Zhang

, Zhang

G Z

, Liu

H F

Study on microstructure and properties of medium carbon steel wire drawing process

[J]. Met. Prod., 2020, 46(1): 14

[本文引用: 2]

张伦, 张国珍, 刘红芳.

中碳钢丝拉拔过程组织与性能研究

[J]. 金属制品, 2020, 46(1): 14

[本文引用: 2]

[21]

Jiang

K C

. Wire Drawing Technique [M]. Beijing: Light Industry Press, 1982

蒋克昌

. 钢丝拉拔技术 [M]. 北京: 轻工业出版社, 1982

[22]

Zhou

, Zhang

, Wang

, et al.

Crystal plasticity analysis of cylindrical holes and their effects on the deformation behavior of Ni-based single-crystal superalloys with different secondary orientations

[J]. Int. J. Plast., 2019, 119: 249

[23]

Zhang

X D

, Godfrey

, Hansen

, et al.

Evolution of cementite morphology in pearlitic steel wire during wet wire drawing

[J]. Mater. Charact., 2010, 61(1): 65

[24]

Franciosi

, Le

L T

, Monnet

, et al.

Investigation of slip system activity in iron at room temperature by SEM and AFM in-situ tensile and compression tests of iron single crystals

[J]. Int. J. Plast., 2015, 65: 226

[25]

Kumar

, Gurao

N P

, Haldar

, et al.

Progressive changes in the microstructure and texture in pearlitic steel during wire drawing

[J]. ISIJ Int., 2011, 51(4): 679

DOI URL

[26]

Watanabe

Possible slip systems in body centered cubic iron

[J]. Mater. Trans., 2006, 47(8): 1886

DOI URL

[27]

Min

K M

, Jeong

, Hong

S H

, et al.

Integrated crystal plasticity and phase field model for prediction of recrystallization texture and anisotropic mechanical properties of cold-rolled ultra-low carbon steels

[J]. Int. J. Plast., 2020, 127: 102644

DOI URL [本文引用: 2]

[28]

Pokharel

, Patra

, Brown

D W

, et al.

An analysis of phase stresses in additively manufactured 304L stainless steel using neutron diffraction measurements and crystal plasticity finite element simulations

[J]. Int. J. Plast., 2019, 121: 201

[29]

Sun

F W

, Meade

E D

, O'dowd

N P

Strain gradient crystal plasticity modelling of size effects in a hierarchical martensitic steel using the Voronoi tessellation method

[J]. Int. J. Plast., 2019, 119: 215

[30]

Huang

X T

, Wang

J J

, Zhao

S X

, et al.

High-resolution multiscale modeling of mechanical behavior of cold-drawn pearlitic steels

[J]. J. Mater. Res. Technol., 2021, 15: 5920

[31]

Zhao

J W

, Jiang

Z Y

, Wang

Z H

, et al.

An analysis of micro deep drawing of ferritic stainless steel 430 using crystal plasticity finite element method

[J]. J. Mater. Res. Technol., 2022, 20: 2247

[32]

Zheng

Z B

, Zhao

P D

, Zhan

, et al.

The roles of rise and fall time in load shedding and strain partitioning under the dwell fatigue of titanium alloys with different microstructures

[J]. Int. J. Plast., 2022, 149: 103161

[33]

Zhang

W T

, Jiang

, Zhao

, et al.

Effects of temperature and microstructure on low cycle fatigue behaviour of a PM Ni-based superalloy: EBSD assessment and crystal plasticity simulation

[J]. Int. J. Fatigue, 2022, 159: 106818

[34]

Schmitt

J H

, Shen

E L

, Raphanel

J L

A parameter for measuring the magnitude of a change of strain path: validation and comparison with experiments on low carbon steel

[J]. Int. J. Plast., 1994, 10(5): 535

[35]

H Y

The effect of annealing process on the microstructures and properties of 2000 MPa cold-drawn steel wire

[J]. Iron Steel Van. Tit., 2022, 43(2): 172

苏红艳

退火工艺对2000 MPa级冷拉钢丝组织和性能的影响

[J]. 钢铁钒钛, 2022, 43(2): 172