树枝晶是一种最常见的合金凝固组织, 其形态和尺度对合金力学性能具有重要影响. 因此, 长期以来人们非常重视对枝晶组织形成过程的研究, 期望能通过合理设计凝固工艺来调整合金凝固组织, 达到控制合金材料性能的目的.
枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高.
近年来, CA模拟方法在合金凝固过程研究中的应用受到人们关注, 相关模型发展很快. 本文将综述枝晶生长CA模型及模拟方法的发展历程, 并展望了模型的未来发展方向.
1 元胞自动机模拟过程及关键参数计算方法
元胞自动机模拟的一般过程为: 将所要模拟的区域划分成有限个规则排列, 且尺寸和结构相同的元胞, 每个元胞储存元胞的状态值, 如温度、溶质浓度、固相体积分数(通常假设1为固相, 0为液相, 0~1为界面)、生长取向、液相流速等一些物理量, 固液界面在一个元胞之内, 只有界面元胞可以生长. 通过求解温度场和浓度场控制方程, 并耦合枝晶生长动力学计算, 确定每一时刻各元胞的温度、浓度、生长速度、固相体积分数等参量. 界面元胞下一时刻的状态由此时刻本身的状态和其邻居元胞的状态按一定的转换规则确定. 液态元胞被捕获变为界面元胞后, 具有与母胞相同的生长取向, 界面元胞可以生长并具有捕获其它液态元胞的能力.
1.1 邻居构型
在CA方法中, 元胞的邻居构型决定了元胞所处的局部环境, 进而影响元胞的演变行为. 二维CA元胞网格常用邻居构型关系如图1所示. 只考虑最近邻的邻居构型称为Von Neumann四邻居构型, 考虑最近邻和次近邻的邻居构型称为Moore八邻居构型. 三维CA元胞网格中的邻居构型关系如图2所示[8 ] . 根据元胞之间的位置关系, 可以将邻居元胞分为最近邻、次近邻和第三近邻3类, 模拟中通常使用将3类邻居都考虑在内的26邻居构型.
图1 二维正方形CA体系常用邻居构型
Fig.1 Neighbors of the cell A in 2D square mesh(a) Von Neumann (b) Moore
图2 三维立方CA体系中的邻居构型[8 ]
Fig.2 Fig.2 Neighbors of the cell A in 3D cubic mesh[8 ] (a) the nearest neighbors of the cell A (I)(b~d) the second nearest neighbors of the cell A (II)(e, f) the third nearest neighbors of the cell A (III)
1.2 形核
根据经典形核理论, 均质形核和非均质形核的形核率 Ihomo 和 Iheter 分别为[9 ] :
式中, Δ G * B 为 Boltzmann常数, I 0 h o m o I 0 h e t e r
在实际凝固过程中, 非均质形核较为常见, CA模拟中常用基于实验数据的瞬时形核模型和连续形核模型处理非均质形核过程.
瞬时形核模型假设所有晶核在同一过冷度下形成, 形核过程是瞬时完成的.
基于实验数据, Hunt[10 ] 用下式处理形核过程:
式中, K1 为常数, ns 为非均质形核基底密度, n(t)为t 时刻的晶核密度. 参数ns 和 θ需由实验确定.
Stefanescu等[11 ] 在Hunt[10 ] 工作的基础上, 提出了如下形核模型:
式中, I 是形核率,K2 和K3 为常数, ΔT为过冷度, ΔTn 为初始形核过冷度, d为原子直径,nsl 为单位体积液体内在形核基底表面上的原子数,D是扩散系数.
瞬时形核模型只适用于熔体中只存在一种异质形核质点, 而且所有质点尺寸相同的情形. 实际凝固过程中, 熔体中存在种类、尺寸不同的异质形核质点, 因此, 晶核密度应随温度连续变化.
连续形核模型假设晶核密度连续地依赖于过冷度, 形核过程在一定的温度范围连续完成.
Oldfield[12 ] 基于异质形核质点连续分布的概念, 提出如下形核模型:
式中, K 4
Rappaz和Gandin[13 ] 基于Oldfield[12 ] 的连续形核思想, 将某一过冷度 Δ T n ( Δ T )
此分布函数可以用如图3[13 ] 所示的Gauss分布来表示, 表达式如下:
式中, n m a x Δ T m a x Δ T σ
这些形核模型均是在实验基础上得出的, 都能用来模拟形核过程. 模拟时选择何种模型的关键是考察哪个模型能与实际情况符合得更好. 通常, 对于凝固温度区间较小的合金, 用瞬时模型较好, 该模型简单, 可节省计算时间. 关于形核位置的确定, 目前数值模拟中通常采用基于概率的随机选择方法[14 -16 ] .
需要指出的是, 在实际凝固过程中, 晶核形成后可能会熔化消失, 枝晶生长时也会发生枝晶熔断而产生新的晶核, 凝固后的晶粒密度与形核产生的晶核密度并不一定相等. 因此, 虽然应用以上模型能够得到与实验相符的模拟结果, 但并不能准确反映枝晶组织的实际形成过程.
图3 型壁和熔体内的非均匀形核[13 ]
Fig.3 Distribution of the heterogeneous nucleation sites on the mold wall and in the bulk melt (The subscripts s and v represent the nucleation on the mold wall and in the bulk melt, respectively. ΔTs, max and ΔTv, max are mean undercooling, ΔTs, σ and ΔTv, σ are standard deviation, ns and nv are total density of grains)[13 ]
1.3 生长速度
常用解析模型和守恒模型2种方法计算枝晶生长速度. 解析模型可分为KGT模型和Sharp interface模型2类. KGT模型[17 ] 基于界面稳定性理论给出枝晶尖端半径、枝晶尖端生长速度与界面前沿过冷度的关系. 应用时通常将枝晶尖端生长速度 v t Δ T [18 ] :
式中, α 1 α 2
该方法只适用于恒定过冷度下枝晶稳态生长时尖端生长速度的计算, 不适用于计算尖端以外界面的生长速度. 而实际凝固过程中, 在枝晶达到稳态生长之前要经历非稳态生长过程, 且枝晶各个部分的过冷度是不同的, 所以不能用KGT模型计算整个枝晶界面的生长速度.
图4 固液界面生长方向示意图
Fig.4 Schematic diagram of the S/L interface growth direction(n ^ φ is the angle between n ^ θ0 is the anglebetween the crystallographic orientation and x axis)
Sharp interface模型[19 ] 用下式计算固液界面法向生长速度:
式中, v n μ 为动力学系数.
对于树枝晶生长, μ 不仅依赖于结晶取向, 而且与温度有关, 其确定极为困难. 应用时通常通过将 μ 乘以一个各向异性函数来表示结晶取向的影响.
守恒模型基于枝晶生长时界面处溶质或能量守恒关系计算固液界面生长速度, 能够较合理地描述固液界面推进速率.
式中, C L * k 0 D L D S n ^ n ^ = ∇ f S ∇ f S f S Δ H α S α L
1.4 界面能各向异性
沿不同晶体学方向的固液界面能不同, 枝晶生长特性亦不同. 对于二维体系, 固液界面能 σ ( ϕ , θ 0 )
式中, σ 0 θ 0 x φ x a φ , θ 0
对于具有4重对称的体系, 各向异性函数为[20 ] :
式中, ε
界面能的各向异性影响界面处的局部曲率过冷度, 对于二维体系, 曲率过冷度 Δ T R
式中, K Δ S f
对于三维体系, Δ T R
式中, K 1 * K 2 * φ 1 φ 2 σ φ 1 , φ 2 φ 1 φ 2 a ( n ^ ) [21 ] :
式中, nx ,ny 和nz 为界面法向的Cartesian坐标.
1.5 耦合温度场、浓度场及流场计算
对于给定的合金, 浓度场、温度场和熔体流场决定着合金的凝固过程及组织, 因此, 要真实体现凝固组织形成过程, 必须耦合温度场、浓度场及流场开展模拟.
合金内热传输控制方程为:
式中, u ρ C p λ
合金内溶质传输的控制方程为:
通常人们用有限体积法、有限元法或有限差分法对传热、传质过程控制方程进行离散和数值求解[21 -23 ] .
金属液对流过程控制方程为:
连续性方程
动量方程
式中,P为压力.
一般人们用交错网格的SIMPLE算法[24 ] 求解动量方程和连续性方程, 也可以用Lattice Boltzmann法求解流场[25 ] .
2 CA模型的发展及应用
1993年, Rappaz和Gandin[13 ] 首先建立了研究凝固组织形成过程的二维CA模型. 他们用连续形核模型描述熔体内部及型壁处的形核过程, 随机分配形核位置以及晶粒取向, 用KGT模型计算固液界面生长速度, 算法如图5a所示[13 ] . 在二维平面上, 将计算区域划分为正方的网格单元. A * θ , 固态元胞的取向指数(即上述的正整数)直接与θ 对应. 由于对称关系, θ 的取值范围为-45°<θ <45°, 共分成48个等概率方向, 每个方向之间的夹角小于2°, 形核元胞的晶粒取向从这48个整数中随机选择一个. 晶粒生长过程中, 被捕获的液态元胞与捕获它的固态元胞具有相同的晶粒取向. 晶粒半径 L t t N t 时刻整个时间段上的积分, 即:
图5 2D 正方算法示意图[13 ]
Fig.5 Schematic illustration of the 2D square algorithm (L(t) is the radius of grain, q is the angle between the preferred orientation and the x axis)[13 ]
模拟结果表明, 随着凝固的进行, 枝晶尖端会偏离初始生长方向, 因此需要时时对枝晶尖端进行修正, 如图5b所示[13 ] . 应用此模型, 对小尺寸铸件凝固组织的形成进行了二维模拟, 展示了铸锭凝固过程中柱状晶的竞争生长、CET转变以及等轴晶生长过程中相互碰撞现象. 进而, 用该模型考察了合金成分和冷却速率对Al-Si合金凝固组织的影响, 模拟结果与实验结果相符. 但在该模型中, 假定铸件温度均匀, 没有考虑热传输和结晶潜热的释放, 也没有考虑凝固过程中浓度场的变化, 因而模型与实际情况差别较大.
1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题.
以上的CA模型均采用解析法计算固液界面的推进速率, 只适用于恒定过冷度下枝晶稳态生长时尖端生长速度的计算, 不适于计算尖端以外的界面生长速度. 1997年, Dilthey等[32 ] 提出了基于凝固界面处热量或溶质守恒关系计算枝晶生长速度的元胞自动机模型, 将CA模型的应用范围由介观尺度推进到了微观尺度. 基于界面处热量守恒计算枝晶生长速度的CA模型适用于纯金属或者共晶合金; 基于界面处溶质守恒计算枝晶生长速度的CA模型适用其它合金. 模型中, 假定界面在2个方向上以平面向前移动(图6), 提出用下式计算固相分数增量 Δ f S
图6 固液界面元胞固相分数计算示意图
Fig.6 Illustration of the calculation of solid fraction of an interfacial cell ( Δs is the size of the cell, vx and vy are the velocities along the coordinate axis)
式中, Δ t Δ s v x v y x y
但此种固相分数计算方法只有在固液界面与坐标轴平行或垂直时才比较准确. 同时, 该模型模拟的枝晶只能沿网格轴线生长, 并且模拟结果的准确性受到网格尺寸的限制.
随着CA模拟方法及模型的发展, 人们期待研发更切合实际凝固过程的CA模型. 在凝固组织的形成过程中, 凝固界面前沿的温度场、界面处的溶质再分配和曲率过冷等多个因素均影响着凝固组织的演变和生长动力学. 只有在模型中考虑这些因素的影响, 模拟结果才可能真正反映合金凝固组织形成机制. 在CA模型中常用的界面曲率计算方法有2种. 第一种是元胞计数法[33 ] , 用下式计算界面处的平均曲率:
式中, K为平均曲率, N f S k k - 1 Δ s 1 Δ s
第2种方法将曲率表示为界面单位法向量的散度[34 ] , 赋予其更加明确的物理含义. 对于二维系统, 若将界面轮廓看做一个由连续函数 f S x , y f S x , y x y [35 ] :
1999年, Nastac[36 ] 沿用溶质守恒条件计算固液界面的迁移速度, 进一步发展了CA模型. 模型考虑了枝晶生长过程中界面处的溶质再分配和曲率过冷, 应用元胞计数法计算界面平均曲率, 同时耦合温度场和浓度场计算, 能够反应多个物理量作用下枝晶的形貌演变. 由于考虑了溶质再分配, 该模型可以模拟一次枝晶的生长、二次及三次分支的形成和粗化过程, 并能模拟溶质偏析现象, 改变了以往经典CA模型只能粗略显示微观结构和晶粒组织的困境.
随后, Beltran-Sanchez和Stefanescu (BSS)[37 ] 改进了图6所示的 Δ f S v n Δ t L φ ( 图7)的比值来确定 Δ f S
图7 固相分数增长算法示意图
Fig.7 Calculation of the increment in solid fraction by the motion of planar interface along the normal to the surface (Once the interface covers the distance Lφ ,the cell status becomes solid, n ^
式中, p为0~1的随机数,η为扰动振幅.
Zhu等[18 ,38 -40 ] 在传统的CA模型改进方面做了许多工作. 2001年, Zhu等[18 ] 发展了改进的CA模型(MCA模型), MCA模型保留了传统CA模型中有关非均质形核和晶核的择优生长方向的随机性概念, 但与传统CA模型不同, MCA模型不仅考虑了固液界面的热力学过冷, 还考虑了凝固过程中界面曲率的变化, 溶质再分配以及溶质在固、液两相中的扩散, 结合有限元方法求解模拟区域的温度场及浓度场. 用此模型对SCN-Actone, Al-Cu和Al-Si系合金等轴晶和定向凝固柱状晶组织形成过程开展了模拟研究[18 ,38 ] , 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] .
为了模拟任意择优生长方向的枝晶形貌, 2004年, Zhu等[24 ] 建立了固液界面处连续变化固相分数的计算方法, 通过引入与邻近元胞状态有关的几何因子G, 建立了界面元胞固相分数变化率 ∂ f S ∂ t
式中,b为经验系数, S m I S m I I
由自然对流或强制对流所引起的金属液流动是凝固过程中不可避免的现象, 它会改变凝固过程中合金的浓度场和温度场, 从而影响枝晶生长与形貌. 2004年, Zhu等[24 ] 将MCA模型推广到包含熔体对流的合金凝固过程, 发展了一个二维MCA-传输模型. 该模型将CA的枝晶生长算法与动量和质量传输的数值计算完全耦合起来, 能够模拟二元合金在流场作用下的凝固组织形成过程. 用此模型模拟了流场作用下Al-Cu合金凝固时单枝晶和多枝晶的生长形貌和生长规律, 模拟结果揭示了合金凝固过程中熔体流动、溶质再分配和相变之间的相互作用本质[41 ] .
2007年, Zhu和Stefanescu[42 ] 在BSS的模型基础上, 通过构建虚拟固液界面来模拟任意择优生长方向的枝晶形貌, 同时提出了以固液界面熔体平衡浓度和实际浓度之差作为驱动计算长大速度的新算法:
式中, C L * , e q C L *
改进的模型能够合理地定量描述枝晶从非稳态到稳态的生长过程, 并且计算效率较高.
近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果.
随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性.
早期的CA模型基本上都是针对二元合金系发展起来的, 实际应用的金属材料多为三元或多元合金. 近年来, 研究者们的关注焦点逐渐转向多元合金凝固过程的CA模型. 以往用CA模型模拟二元合金凝固组织形成时, 通常假设液相线斜率和平衡溶质分配系数为常数, 这与实际情况相差较大, 所以要准确计算固液界面溶质成分和溶质再分配过程, 必须耦合合金热力学计算. 2000年, Jarvis等[57 ] 用CAFE模型与商业软件Thermo-Calc相结合, 模拟了Al-Cu-Mg合金凝固过程的偏析, 并对比分析了对1D, 2D和3D凝固组织的模拟结果. 2007年, Zhu等[58 ] 借助于热力学软件PanEngine计算了多元合金的平衡液相线温度和平衡固相浓度, 在进行CA模拟时, 通过查表插值得到所需数据, 实现了动力学与热力学的弱耦合模拟.
实际上, 要真正反映凝固过程中合金成分变化的轨迹, 真实地再现多元合金凝固过程, 必须直接耦合计算合金热力学与凝固动力学. 此外, 在已往的模拟中, 人们通常假设溶质扩散系数为常数或者只依赖于温度, 忽略了合金成分的影响. 这对二元合金凝固过程模拟可以接受, 但对多元合金来说, 误差较大. 据此, 张显飞[59 ] 在考虑组元间相互作用的基础上建立了多元合金树枝晶生长的三维元胞自动机模型(3D CA), 并研发了直接耦合合金热力学与凝固动力学计算的模拟方法. 应用该模型模拟了Al-Cu-Mg合金定向凝固组织形成过程, 清晰地展示了枝晶生长过程, 如图8所示, 模拟预测与实验结果吻合得很好, 如图9所示. 模拟结果表明, 溶质扩散系数与合金成分有关, 合金元素间相互作用显著影响合金凝固过程, 如图10所示.
图8 Al-11.6%Cu-0.85%Mg合金定向凝固组织演变过程[59 ]
Fig.8 Microstructural evolution in directionally solidified Al-11.6%Cu-0.85%Mg alloy (The temperature gradient in front of the S/L interface is 10 K/mm)[59 ] (a) t =1.3 s (b) t =2.7 s (c) t =4 s (d) t =8.7 s (e) t =10.7 s
图9 定向凝固Al-11.6Cu-0.85Mg合金枝晶间距[59 ]
Fig.9 Dendrite spacing l for directionally solidified Al-11.6Cu-0.85Mg alloys[59 ]
图10 应用不同溶质扩散系数处理方法时计算的枝晶尖端生长速度随时间的变化[59 ]
Fig.10 Dendrite tip velocities calculated using different diffusion coefficients (Line 1 is the results calculated using the diffusion coefficients considering solute interactions, line 2 is the results calculated using the diffusion coefficients neglecting solute interactions)[59 ]
3 展望
元胞自动机方法能有效地模拟合金凝固过程, 相关模型的研发已取得了很大进展, 但还存在一些问题, 主要如下:
(1) 现存的CA模型尚不能真实地描述所有实际凝固条件下合金的凝固过程, 还需要进一步发展、充实与完善. 例如, 目前的CA模型均是针对近平衡凝固体系建立的, 不能描述大过冷度条件下的凝固过程; 又如, 实际凝固过程中会发生枝晶熔断现象, 即局部会发生固相向液相转变, 现有的CA模型没有考虑固相熔化问题, 不能再现枝晶熔断及其导致的枝晶粗化现象.
(2) 某些物理参数的计算尚需优化. 例如, 固相分数增量和凝固界面曲率的计算还有待完善, 需发展更严密的计算方法, 以减小人为网格各向异性的作用, 使模型能够更精确地再现任意择优生长方向的枝晶形貌.
(3) 加强模型的实用化开发, 结合工业生产实际开展建模与模拟研究, 促进模型的发展与完善, 增强模型的实用性.
参考文献
文献选项
[1]
Wheeler A A Murray B T Schaefer R J Physica , 1993 ; 66D : 243
[本文引用: 1]
[2]
Warren J A Boettinger W J Acta Metall Mater , 1995 ; 43 : 689
[3]
Zhang R J Jing T Jie W Q Liu B C Acta Mater , 2006 ; 54 : 2235
[本文引用: 1]
[4]
McCarthy J F Blake N W Acta Mater , 1996 ; 44 : 2093
[本文引用: 1]
[5]
Juric D Tryggvason G J Comput Phys , 1996 ; 123 : 127
[6]
Zhao P Venere M Heinrich J C Porier D R J Comput Phys , 2003 ; 183 : 434
[本文引用: 1]
[7]
Liu Y Xu Q Y Liu B C Tsinghua Sci Technol , 2006 ; 5 : 495
[本文引用: 1]
[8]
Jiang H X Zhao J Z Acta Metall Sin , 2011 ; 47 : 1099
[本文引用: 4]
(江鸿翔 ,赵九洲 . 金属学报 , 2011 ; 47 : 1099 )
[本文引用: 4]
[9]
Turnbull D J J Chem Phys , 1952 ; 20 : 411
[本文引用: 1]
[10]
Hunt J D Mater Sci Eng , 1984 ; 65 : 75
[本文引用: 2]
[11]
Stefanescu D M Upadhya G Bandyopadhyay D Metall Trans , 1990 ; 21A : 997
[本文引用: 1]
[12]
Oldfield W Trans ASM , 1966 ; 59 : 945
[本文引用: 2]
[13]
Rappaz M Gandin C A Acta Metall Mater , 1993 ; 41 : 345
[本文引用: 9]
[14]
Yao X Dargusch M S Dahle A K Davidson C J Stjohn D H J Mater Res , 2008 ; 23 : 2312
[本文引用: 1]
[15]
Cho S H Okanem T Umeda T Sci Technol Adv Mater , 2002 ; 2 : 241
[16]
Dong H B Lee P D Acta Metall , 2005 ; 53 : 659
[本文引用: 1]
[17]
Kurz W Giovanola B Trivedi R Acta Metall , 1986 ; 34 : 823
[本文引用: 1]
[18]
Zhu M F Kim J M Hong C P ISIJ Int , 2001 ; 41 : 992
[本文引用: 4]
[19]
Sekerka R F J Cryst Growth , 2004 ; 264 : 530
[本文引用: 1]
[20]
Beltran-Sanchez L Stefanescu D M Metall Mater Trans , 2004 ; 35A : 2471
[本文引用: 1]
[21]
Pan S Y Zhu M F Acta Metall , 2010 ; 58 : 340
[本文引用: 2]
[22]
Gandin C A Rappaz M Acta Metall Mater , 1994 ; 42 : 2233
[本文引用: 1]
[23]
Rappaz M Gandin C A Desbiolles J L Thevoz P Metall Mater Trans , 1996 ; 27A : 695
[本文引用: 2]
[24]
Zhu M F Lee S Y Hong C P Phys Rev , 2004 ; 69E : 061610
[本文引用: 3]
[25]
Yin H Felicelli S D Wang L Acta Mater , 2011 ; 59 : 3124
[本文引用: 2]
[26]
Gandin C A Rappaz M Acta Mater , 1997 ; 45 : 2187
[本文引用: 2]
[27]
Dong H B Lee P D Acta Mater , 2005 ; 53 : 659
[本文引用: 1]
[28]
Brown S G R , Spittle J A Williams T Acta Metall Mater , 1994 ; 42 : 2893
[本文引用: 1]
[29]
Spittle J A Brown S G R . J Mater Sci , 1995 ; 30 : 3989
[本文引用: 1]
[30]
Gandin C A Rappaz M Tintillier R Metall Mater Trans , 1993 ; 24 : 467
[本文引用: 1]
[31]
Gandin C A Desbiolles J L Rappaz M Thevoz P Metall Mater Trans , 1999 ; 30A : 3153
[本文引用: 1]
[32]
Dilthey U Pavlik V Reichel T In: Cerjak H, Bhadeshia H K D H eds., Mathematical Modeling of Weld Phenomena 3. London: The Institute of Materials , 1997 : 85
[本文引用: 1]
[33]
Sasikumar R Sreenivasan R Acta Metall Mater , 1994 ; 42 : 2381
[本文引用: 1]
[34]
Kothe D B Mjolsness R C Torrey M D Ripple: A Computer Program for Incompressible Flows with Free Surface. Los Alamos: Los Alamos National Lab , 1991 : 1
[本文引用: 1]
[35]
Beltran-Sanchez L Stefanescu D M Metall Mater Trans , 2003 ; 34A : 367
[本文引用: 1]
[36]
Nastac L Acta Mater, l999 ; 47 : 4253
[本文引用: 1]
[37]
Beltran-Sanchez L Stefanescu D M Metall Mater Trans , 2004 ; 35A : 2471
[本文引用: 1]
[38]
Zhu M F Hong C P ISIJ Int , 2001 ; 41 : 436
[本文引用: 2]
[39]
Zhu M F Hong C P Phys Rev , 2002 ; 66 : 155428
[本文引用: 1]
[40]
Zhu M F Hong C P ISIJ Int , 2002 ; 42 : 520
[本文引用: 2]
[41]
Zhu M F Dai T Li C Y Hong C P Sci China E , 2005 ; 35E : 67
[本文引用: 1]
(朱鸣芳 , 戴 挺 , 李成允 , 洪俊杓 . 中国科学E , 2005 ; 35 : 673 ) url:
URL
[本文引用: 1]
[42]
Zhu M F Stefanescu D M Acta Mater , 2007 ; 55 : 1741
[本文引用: 1]
[43]
Li Q Li D Z Qian B N Acta Metall Sin , 2004 ; 40 : 634
[本文引用: 1]
(李 强 , 李殿中 , 钱百年 . 金属学报 , 2004 ; 40 : 634 )
[本文引用: 1]
[44]
Li Q Li D Z Qian B N Acta Metall Sin , 2004 ; 40 : 1215
[本文引用: 1]
(李 强 , 李殿中 , 钱百年 . 金属学报 , 2004 ; 40 : 1215 )
[本文引用: 1]
[45]
Wei L Lin X Wang M Huang W D Acta Phys Sin , 2012 ; 61 : 098104
[本文引用: 1]
(魏 雷 , 林 鑫 , 王 猛 , 黄卫东 . 物理学报 , 2012 ; 61 : 098104 )
[本文引用: 1]
[46]
Lin X Wei L Shan B W Huang W D In: Howard J ed., Proc 5th Decennial International Conference on Solidification Processing, Sheffield: University of Sheffield , 2007 : 53
[本文引用: 1]
[47]
Lin X Wei L Wang M Huang W D Mater Sci Forum, 2010: 654 -656 : 1528
[本文引用: 1]
[48]
Fu Z N Xu Q Y Xiong S M Chin J Nonferrous Met , 2007 ; 17 : 1567
[本文引用: 1]
(付振南 , 许庆彦 , 熊守美 . 中国有色金属学报 , 2007 ; 17 : 1567 )
[本文引用: 1]
[49]
Marek M Physica , 2013 ; 253D : 73
[本文引用: 1]
[50]
Li D Z Su S F Xu X H Wang J Q Chen J Z Liu Y M Foundary , 1997 ; (8 ): 1
[本文引用: 1]
(李殿中 , 苏仕方 , 徐雪华 , 王君卿 , 陈家芝 , 刘一鸣 . 铸造 , 1997 ; (8 ): 1 )
[本文引用: 1]
[51]
Li D Z Du Q Hu Z Y Li Y Y Acta Metall Sin , 1999 ; 39 : 1201
[本文引用: 1]
(李殿中 , 杜 强 , 胡志勇 , 李依依 . 金属学报 , 1999 ; 39 : 1201 )
[本文引用: 1]
[52]
Kang X H Du Q Li D Z Acta Metall Sin , 2004 ; 40 : 452
[本文引用: 1]
(康秀红 , 杜强 , 李殿中 . 金属学报 , 2004 ; 40 : 452 )
[本文引用: 1]
[53]
Yin H Felicelli S D Acta Mater , 2010 ; 58 : 1455
[本文引用: 1]
[54]
Shi Y F Xu Q Y Gong M Liu B C Acta Metall Sin , 2011 ; 47 : 620
[本文引用: 1]
(石玉峰 , 许庆彦 , 龚 铭 , 柳百成 . 金属学报 , 2011 ; 47 : 620 )
[本文引用: 1]
[55]
Zaeem M A Yin H Felicelli S D J Mater Sci Technol , 2012 ; 28 : 137
[本文引用: 1]
[56]
Zaeem M A Yin H Felicelli S D Appl Math Modell , 2013 ; 37 : 3495
[本文引用: 1]
[57]
Jarvis D J Brown S G R , Spittle J A Mater Sci Technol , 2000 ; 16 : 1420
[本文引用: 1]
[58]
Zhu M F Cao W Chen S L Hong C P Chang Y A J Phase Equilib Diffus , 2007 ; 28 : 130
[本文引用: 1]
[59]
Zhang X F PhD Dissertation, Institute of Metal Research, Chinese Academy of Sciences, Shenyang , 2012
[本文引用: 7]
(张显飞 . 中国科学院金属研究所博士学位论文, 沈阳 , 2012 )
[本文引用: 7]
1
1993
... 枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. ...
1
2006
... 枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. ...
1
1996
... 枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. ...
1
2003
... 枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. ...
1
2006
... 枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. ...
4
2011
... 枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. ...
... 在CA方法中, 元胞的邻居构型决定了元胞所处的局部环境, 进而影响元胞的演变行为. 二维CA元胞网格常用邻居构型关系如图1所示. 只考虑最近邻的邻居构型称为Von Neumann四邻居构型, 考虑最近邻和次近邻的邻居构型称为Moore八邻居构型. 三维CA元胞网格中的邻居构型关系如图2所示[8 ] . 根据元胞之间的位置关系, 可以将邻居元胞分为最近邻、次近邻和第三近邻3类, 模拟中通常使用将3类邻居都考虑在内的26邻居构型. ...
... Fig.2 Neighbors of the cell A in 3D cubic mesh[8 ] ...
... 三维立方CA体系中的邻居构型[8 ] ...
4
2011
... 枝晶组织形成机理的研究方法可分为3类: 实验法、解析法和数值模拟法. 由于合金不透明, 合金凝固组织形成过程的实验研究极为困难. 人们通常通过观察物理性质与合金相近的有机物溶液(透明合金)的凝固过程来了解合金凝固过程. 解析法通常只能给出稳态生长时枝晶尖端形态的解, 无法对二次分枝、三次分枝的形成与生长, 以及整个枝晶形态演变进行描述. 数值模拟方法通过计算温度场、浓度场和枝晶生长来研究凝固组织的演变, 可以直观地再现树枝晶生长过程和整个树枝晶形态, 是研究枝晶组织形成的有效手段. 目前常用的数值模拟方法有相场法(PF), 界面跟踪法(FT)和元胞自动机法(CA). PF模型用连续变化的相场参数描述固液界面的移动, 避免了显性跟踪固液界面位置, 能模拟复杂的枝晶形态. 但受网格尺寸的限制, 相场模型的计算量较大、占用计算机内存较大、计算效率较低, 通常只能模拟很小区域内的枝晶生长过程[1 -3 ] , FT法基于尖锐界面(sharp interface)模型计算固液界面生长速度, 通过定义固液界面位置的标志变量, 显性跟踪每一时刻固液界面位置和形态, 能很好地描述枝晶的形成和生长过程, 在模拟树枝晶生长、柱状晶向等轴晶转变(CET)以及等轴晶生长等方面应用较多[4 -6 ] , 但该方法跟踪界面位置的数值算法非常复杂, 且计算效率低, 不适于模拟实际凝固条件下多枝晶的生长过程. CA法将模拟区域离散成有限个单元(元胞), 分为固态、液态和界面3类元胞. 各类元胞之间根据一定的规则进行转化, 从而模拟合金凝固过程[7 ,8 ] . 与其它模型相比, CA模型能够充分地考虑影响枝晶生长的各种物理机制, 与具有明确物理意义的参数相结合, 算法简单, 计算效率较高. ...
... 在CA方法中, 元胞的邻居构型决定了元胞所处的局部环境, 进而影响元胞的演变行为. 二维CA元胞网格常用邻居构型关系如图1所示. 只考虑最近邻的邻居构型称为Von Neumann四邻居构型, 考虑最近邻和次近邻的邻居构型称为Moore八邻居构型. 三维CA元胞网格中的邻居构型关系如图2所示[8 ] . 根据元胞之间的位置关系, 可以将邻居元胞分为最近邻、次近邻和第三近邻3类, 模拟中通常使用将3类邻居都考虑在内的26邻居构型. ...
... Fig.2 Neighbors of the cell A in 3D cubic mesh[8 ] ...
... 三维立方CA体系中的邻居构型[8 ] ...
1
1952
... 根据经典形核理论, 均质形核和非均质形核的形核率 Ihomo 和 Iheter 分别为[9 ] : ...
2
1984
... 基于实验数据, Hunt[10 ] 用下式处理形核过程: ...
... Stefanescu等[11 ] 在Hunt[10 ] 工作的基础上, 提出了如下形核模型: ...
1
1990
... Stefanescu等[11 ] 在Hunt[10 ] 工作的基础上, 提出了如下形核模型: ...
2
1966
... Oldfield[12 ] 基于异质形核质点连续分布的概念, 提出如下形核模型: ...
... Rappaz和Gandin[13 ] 基于Oldfield[12 ] 的连续形核思想, 将某一过冷度 Δ T n ( Δ T )
9
1993
... Rappaz和Gandin[13 ] 基于Oldfield[12 ] 的连续形核思想, 将某一过冷度 Δ T n ( Δ T )
... 此分布函数可以用如图3[13 ] 所示的Gauss分布来表示, 表达式如下: ...
... Distribution of the heterogeneous nucleation sites on the mold wall and in the bulk melt (The subscripts s and v represent the nucleation on the mold wall and in the bulk melt, respectively. ΔTs, max and ΔTv, max are mean undercooling, ΔTs, σ and ΔTv, σ are standard deviation, ns and nv are total density of grains)[13 ] ...
... 型壁和熔体内的非均匀形核[13 ] ...
... 1993年, Rappaz和Gandin[13 ] 首先建立了研究凝固组织形成过程的二维CA模型. 他们用连续形核模型描述熔体内部及型壁处的形核过程, 随机分配形核位置以及晶粒取向, 用KGT模型计算固液界面生长速度, 算法如图5a所示[13 ] . 在二维平面上, 将计算区域划分为正方的网格单元. A * θ , 固态元胞的取向指数(即上述的正整数)直接与θ 对应. 由于对称关系, θ 的取值范围为-45°<θ <45°, 共分成48个等概率方向, 每个方向之间的夹角小于2°, 形核元胞的晶粒取向从这48个整数中随机选择一个. 晶粒生长过程中, 被捕获的液态元胞与捕获它的固态元胞具有相同的晶粒取向. 晶粒半径 L t t N t 时刻整个时间段上的积分, 即: ...
... [13 ]. 在二维平面上, 将计算区域划分为正方的网格单元. A * θ , 固态元胞的取向指数(即上述的正整数)直接与θ 对应. 由于对称关系, θ 的取值范围为-45°<θ <45°, 共分成48个等概率方向, 每个方向之间的夹角小于2°, 形核元胞的晶粒取向从这48个整数中随机选择一个. 晶粒生长过程中, 被捕获的液态元胞与捕获它的固态元胞具有相同的晶粒取向. 晶粒半径 L t t N t 时刻整个时间段上的积分, 即: ...
... Schematic illustration of the 2D square algorithm (L(t) is the radius of grain, q is the angle between the preferred orientation and the x axis)[13 ] ...
... 2D 正方算法示意图[13 ] ...
... 模拟结果表明, 随着凝固的进行, 枝晶尖端会偏离初始生长方向, 因此需要时时对枝晶尖端进行修正, 如图5b所示[13 ] . 应用此模型, 对小尺寸铸件凝固组织的形成进行了二维模拟, 展示了铸锭凝固过程中柱状晶的竞争生长、CET转变以及等轴晶生长过程中相互碰撞现象. 进而, 用该模型考察了合金成分和冷却速率对Al-Si合金凝固组织的影响, 模拟结果与实验结果相符. 但在该模型中, 假定铸件温度均匀, 没有考虑热传输和结晶潜热的释放, 也没有考虑凝固过程中浓度场的变化, 因而模型与实际情况差别较大. ...
1
2008
... 这些形核模型均是在实验基础上得出的, 都能用来模拟形核过程. 模拟时选择何种模型的关键是考察哪个模型能与实际情况符合得更好. 通常, 对于凝固温度区间较小的合金, 用瞬时模型较好, 该模型简单, 可节省计算时间. 关于形核位置的确定, 目前数值模拟中通常采用基于概率的随机选择方法[14 -16 ] . ...
1
2005
... 这些形核模型均是在实验基础上得出的, 都能用来模拟形核过程. 模拟时选择何种模型的关键是考察哪个模型能与实际情况符合得更好. 通常, 对于凝固温度区间较小的合金, 用瞬时模型较好, 该模型简单, 可节省计算时间. 关于形核位置的确定, 目前数值模拟中通常采用基于概率的随机选择方法[14 -16 ] . ...
1
1986
... 常用解析模型和守恒模型2种方法计算枝晶生长速度. 解析模型可分为KGT模型和Sharp interface模型2类. KGT模型[17 ] 基于界面稳定性理论给出枝晶尖端半径、枝晶尖端生长速度与界面前沿过冷度的关系. 应用时通常将枝晶尖端生长速度 v t Δ T [18 ] : ...
4
2001
... 常用解析模型和守恒模型2种方法计算枝晶生长速度. 解析模型可分为KGT模型和Sharp interface模型2类. KGT模型[17 ] 基于界面稳定性理论给出枝晶尖端半径、枝晶尖端生长速度与界面前沿过冷度的关系. 应用时通常将枝晶尖端生长速度 v t Δ T [18 ] : ...
... Zhu等[18 ,38 -40 ] 在传统的CA模型改进方面做了许多工作. 2001年, Zhu等[18 ] 发展了改进的CA模型(MCA模型), MCA模型保留了传统CA模型中有关非均质形核和晶核的择优生长方向的随机性概念, 但与传统CA模型不同, MCA模型不仅考虑了固液界面的热力学过冷, 还考虑了凝固过程中界面曲率的变化, 溶质再分配以及溶质在固、液两相中的扩散, 结合有限元方法求解模拟区域的温度场及浓度场. 用此模型对SCN-Actone, Al-Cu和Al-Si系合金等轴晶和定向凝固柱状晶组织形成过程开展了模拟研究[18 ,38 ] , 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] . ...
... [18 ]发展了改进的CA模型(MCA模型), MCA模型保留了传统CA模型中有关非均质形核和晶核的择优生长方向的随机性概念, 但与传统CA模型不同, MCA模型不仅考虑了固液界面的热力学过冷, 还考虑了凝固过程中界面曲率的变化, 溶质再分配以及溶质在固、液两相中的扩散, 结合有限元方法求解模拟区域的温度场及浓度场. 用此模型对SCN-Actone, Al-Cu和Al-Si系合金等轴晶和定向凝固柱状晶组织形成过程开展了模拟研究[18 ,38 ] , 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] . ...
... [18 ,38 ], 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] . ...
1
2004
... Sharp interface模型[19 ] 用下式计算固液界面法向生长速度: ...
1
2004
... 对于具有4重对称的体系, 各向异性函数为[20 ] : ...
2
2010
... 式中, K 1 * K 2 * φ 1 φ 2 σ φ 1 , φ 2 φ 1 φ 2 a ( n ^ ) [21 ] : ...
... 通常人们用有限体积法、有限元法或有限差分法对传热、传质过程控制方程进行离散和数值求解[21 -23 ] . ...
1
1994
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
2
1996
... 通常人们用有限体积法、有限元法或有限差分法对传热、传质过程控制方程进行离散和数值求解[21 -23 ] . ...
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
3
2004
... 一般人们用交错网格的SIMPLE算法[24 ] 求解动量方程和连续性方程, 也可以用Lattice Boltzmann法求解流场[25 ] . ...
... 为了模拟任意择优生长方向的枝晶形貌, 2004年, Zhu等[24 ] 建立了固液界面处连续变化固相分数的计算方法, 通过引入与邻近元胞状态有关的几何因子G, 建立了界面元胞固相分数变化率 ∂ f S ∂ t
... 由自然对流或强制对流所引起的金属液流动是凝固过程中不可避免的现象, 它会改变凝固过程中合金的浓度场和温度场, 从而影响枝晶生长与形貌. 2004年, Zhu等[24 ] 将MCA模型推广到包含熔体对流的合金凝固过程, 发展了一个二维MCA-传输模型. 该模型将CA的枝晶生长算法与动量和质量传输的数值计算完全耦合起来, 能够模拟二元合金在流场作用下的凝固组织形成过程. 用此模型模拟了流场作用下Al-Cu合金凝固时单枝晶和多枝晶的生长形貌和生长规律, 模拟结果揭示了合金凝固过程中熔体流动、溶质再分配和相变之间的相互作用本质[41 ] . ...
2
2011
... 一般人们用交错网格的SIMPLE算法[24 ] 求解动量方程和连续性方程, 也可以用Lattice Boltzmann法求解流场[25 ] . ...
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
2
1997
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
... [26 ]于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
1
2005
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
1
1994
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
1
1995
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
1
1993
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
1
1999
... 1994年, Gandin和Rappaz[22 ] 提出了2D 长方形算法, 将CA模型与有限元方法(FEM)耦合起来, 建立了CAFE模型. 该模型用有限元方法计算宏观热传输, 用CA模型计算固相形核与长大, 从而使CA模型适用于模拟非均匀温度场内的合金凝固过程, 扩大了模型的应用范围. 用该模型模拟了二维不均匀温度场中晶粒组织形成过程、柱状晶竞争生长及CET转变, 并与商业软件3-Mos相结合[23 ] , 模拟了定向凝固涡轮叶片、连铸杆件等铸件的晶粒结构和激光表面重熔凝固组织. 进而, Gandin和Rappaz[26 ] 提出了偏心四边形算法, 通过对枝晶尖端生长方向的修订, 避免了枝晶在生长过程中偏离初始方向. 此后, Dong和Lee[27 ] 改进了偏心四边形算法, 加入了晶体取向的影响, 模拟了枝晶低速生长以及镍基高温合金定向凝固时的CET转变. Brown等[28 ] 发展了描述自由枝晶稳态生长的2D CA模型. 模型假设枝晶生长由热扩散控制, 考虑了结晶潜热和曲率过冷的影响. 用该模型模拟了不同温度下丁二腈自由枝晶的稳态生长, 得到了枝晶尖端稳态生长速率与尖端过冷度的关系, 模拟结果与实验结果相吻合. 进而, 用此模型模拟了二元合金柱状晶生长, 探索了合金成分、温度梯度以及凝固速率对枝晶间距和枝晶形貌的影响, 模拟结果与实验结果及理论预测相吻合[29 ] . Gandin等[30 ] 基于简化的捕获规则, 将此前的二维CA模型拓展到三维. 该模型用八面体表示晶体形状, 处于八面体内的液态元胞均被捕获并赋予与母胞相同的属性. 模拟结果表明此三维模型接近实际情况. 但此模型仍然假设温度均匀, 其应用受到了限制. 之后Gandin和Rappaz[26 ] 于1997年提出了“偏心八面体”的算法, 进而于1999年提出了3D-CAFE算法[31 ] 并且通过采用动态内存分配, 解决了三维模型计算量大的问题. ...
1
1997
... 以上的CA模型均采用解析法计算固液界面的推进速率, 只适用于恒定过冷度下枝晶稳态生长时尖端生长速度的计算, 不适于计算尖端以外的界面生长速度. 1997年, Dilthey等[32 ] 提出了基于凝固界面处热量或溶质守恒关系计算枝晶生长速度的元胞自动机模型, 将CA模型的应用范围由介观尺度推进到了微观尺度. 基于界面处热量守恒计算枝晶生长速度的CA模型适用于纯金属或者共晶合金; 基于界面处溶质守恒计算枝晶生长速度的CA模型适用其它合金. 模型中, 假定界面在2个方向上以平面向前移动(图6), 提出用下式计算固相分数增量 Δ f S
1
1994
... 随着CA模拟方法及模型的发展, 人们期待研发更切合实际凝固过程的CA模型. 在凝固组织的形成过程中, 凝固界面前沿的温度场、界面处的溶质再分配和曲率过冷等多个因素均影响着凝固组织的演变和生长动力学. 只有在模型中考虑这些因素的影响, 模拟结果才可能真正反映合金凝固组织形成机制. 在CA模型中常用的界面曲率计算方法有2种. 第一种是元胞计数法[33 ] , 用下式计算界面处的平均曲率: ...
1
1991
... 第2种方法将曲率表示为界面单位法向量的散度[34 ] , 赋予其更加明确的物理含义. 对于二维系统, 若将界面轮廓看做一个由连续函数 f S x , y f S x , y x y [35 ] : ...
1
2003
... 第2种方法将曲率表示为界面单位法向量的散度[34 ] , 赋予其更加明确的物理含义. 对于二维系统, 若将界面轮廓看做一个由连续函数 f S x , y f S x , y x y [35 ] : ...
1
... 1999年, Nastac[36 ] 沿用溶质守恒条件计算固液界面的迁移速度, 进一步发展了CA模型. 模型考虑了枝晶生长过程中界面处的溶质再分配和曲率过冷, 应用元胞计数法计算界面平均曲率, 同时耦合温度场和浓度场计算, 能够反应多个物理量作用下枝晶的形貌演变. 由于考虑了溶质再分配, 该模型可以模拟一次枝晶的生长、二次及三次分支的形成和粗化过程, 并能模拟溶质偏析现象, 改变了以往经典CA模型只能粗略显示微观结构和晶粒组织的困境. ...
1
2004
... 随后, Beltran-Sanchez和Stefanescu (BSS)[37 ] 改进了图6所示的 Δ f S v n Δ t L φ ( 图7)的比值来确定 Δ f S
2
2001
... Zhu等[18 ,38 -40 ] 在传统的CA模型改进方面做了许多工作. 2001年, Zhu等[18 ] 发展了改进的CA模型(MCA模型), MCA模型保留了传统CA模型中有关非均质形核和晶核的择优生长方向的随机性概念, 但与传统CA模型不同, MCA模型不仅考虑了固液界面的热力学过冷, 还考虑了凝固过程中界面曲率的变化, 溶质再分配以及溶质在固、液两相中的扩散, 结合有限元方法求解模拟区域的温度场及浓度场. 用此模型对SCN-Actone, Al-Cu和Al-Si系合金等轴晶和定向凝固柱状晶组织形成过程开展了模拟研究[18 ,38 ] , 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] . ...
... ,38 ], 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] . ...
1
2002
... Zhu等[18 ,38 -40 ] 在传统的CA模型改进方面做了许多工作. 2001年, Zhu等[18 ] 发展了改进的CA模型(MCA模型), MCA模型保留了传统CA模型中有关非均质形核和晶核的择优生长方向的随机性概念, 但与传统CA模型不同, MCA模型不仅考虑了固液界面的热力学过冷, 还考虑了凝固过程中界面曲率的变化, 溶质再分配以及溶质在固、液两相中的扩散, 结合有限元方法求解模拟区域的温度场及浓度场. 用此模型对SCN-Actone, Al-Cu和Al-Si系合金等轴晶和定向凝固柱状晶组织形成过程开展了模拟研究[18 ,38 ] , 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] . ...
2
2002
... Zhu等[18 ,38 -40 ] 在传统的CA模型改进方面做了许多工作. 2001年, Zhu等[18 ] 发展了改进的CA模型(MCA模型), MCA模型保留了传统CA模型中有关非均质形核和晶核的择优生长方向的随机性概念, 但与传统CA模型不同, MCA模型不仅考虑了固液界面的热力学过冷, 还考虑了凝固过程中界面曲率的变化, 溶质再分配以及溶质在固、液两相中的扩散, 结合有限元方法求解模拟区域的温度场及浓度场. 用此模型对SCN-Actone, Al-Cu和Al-Si系合金等轴晶和定向凝固柱状晶组织形成过程开展了模拟研究[18 ,38 ] , 并将该模型推广到多相系统的规则、非规则共晶合金[39 ] . 之后, 将MCA模型发展到三维, 模拟了Al-Cu合金雾化液滴的凝固组织形成过程, 与实验结果吻合得很好[40 ] . ...
... [40 ]. ...
1
2005
... 由自然对流或强制对流所引起的金属液流动是凝固过程中不可避免的现象, 它会改变凝固过程中合金的浓度场和温度场, 从而影响枝晶生长与形貌. 2004年, Zhu等[24 ] 将MCA模型推广到包含熔体对流的合金凝固过程, 发展了一个二维MCA-传输模型. 该模型将CA的枝晶生长算法与动量和质量传输的数值计算完全耦合起来, 能够模拟二元合金在流场作用下的凝固组织形成过程. 用此模型模拟了流场作用下Al-Cu合金凝固时单枝晶和多枝晶的生长形貌和生长规律, 模拟结果揭示了合金凝固过程中熔体流动、溶质再分配和相变之间的相互作用本质[41 ] . ...
1
2005
... 由自然对流或强制对流所引起的金属液流动是凝固过程中不可避免的现象, 它会改变凝固过程中合金的浓度场和温度场, 从而影响枝晶生长与形貌. 2004年, Zhu等[24 ] 将MCA模型推广到包含熔体对流的合金凝固过程, 发展了一个二维MCA-传输模型. 该模型将CA的枝晶生长算法与动量和质量传输的数值计算完全耦合起来, 能够模拟二元合金在流场作用下的凝固组织形成过程. 用此模型模拟了流场作用下Al-Cu合金凝固时单枝晶和多枝晶的生长形貌和生长规律, 模拟结果揭示了合金凝固过程中熔体流动、溶质再分配和相变之间的相互作用本质[41 ] . ...
1
2007
... 2007年, Zhu和Stefanescu[42 ] 在BSS的模型基础上, 通过构建虚拟固液界面来模拟任意择优生长方向的枝晶形貌, 同时提出了以固液界面熔体平衡浓度和实际浓度之差作为驱动计算长大速度的新算法: ...
1
2004
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2004
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2004
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2004
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2012
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2012
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2007
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2007
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2007
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
2013
... 近年来, 模拟合金凝固组织演变过程的元胞自动机模型逐渐成熟, 其计算效率高、物理意义明确的特点也逐渐显现. 越来越多的研究者致力于模型的发展和完善, 以期得到更细致、精确的组织形貌, 更深入地研究合金凝固机制. 李强等[43 ,44 ] 采用连续性模型来处理两相界面区域内的物理性质差异, 在固液界面区域内有 ϕ = f S ϕ S + f L ϕ L ϕ f [45 ] 基于界面重构算法, 结合自主开发的zigzag捕获规则[46 ,47 ] , 构建了在细化的界面元胞内重构固液界面位置的二元合金自由枝晶生长CA模型. 该模型可以在较大的网格尺寸下保证模拟结果收敛, 人为网格各向异性不明显、且能反映界面能各向异性对自由枝晶生长的影响. 不同的合金体系具有不同的晶体学特征, 从而与之相适应的CA模型亦不同. 付振南等[48 ] 建立了适合镁合金hcp结构特点的CA模型. 模型耦合了宏观温度场和微观组织模拟计算, 能够模拟镁合金枝晶生长过程. 应用此模型对单个等轴晶生长、多晶粒等轴晶生长及定向凝固柱状晶生长进行了模拟, 模拟结果为实验所验证. 2013年, Marek[49 ] 通过引入生长速率修正因子以及溶质扩散过程的弛豫处理消除了人为网格各向异性的影响, 将模型应用于纯金属凝固过程二维枝晶形貌的模拟, 取得了很好的效果. ...
1
1997
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
1997
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
1999
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
1999
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2004
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2004
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2010
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2011
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2011
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2012
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2013
... 随着有关模型日趋完善, 元胞自动机模拟方法已逐步被应用于研究凝固组织的形成过程及机制. 李殿中等[50 ,51 ] 考虑了非均质形核的机理及影响因素, 用CA方法模拟了镍基合金叶片凝固组织形成过程, 并在此基础上进行了工艺优化研究. 康秀红等[52 ] 用CA与宏观传输场耦合模拟了钢锭凝固组织中的晶粒形貌以及柱状晶-等轴晶转变. Yin和Felicell[53 ] 应用CAFE模型模拟了激光近净成形加工中冷却速率与枝晶间距的关系, 分析了工艺参数对枝晶间距的影响. 此外, 在焊接熔池中的枝晶生长、雾化液滴的凝固等方面CA模型也得到了广泛的应用. 石玉峰等[54 ] 建立了一种改进的CA模型, 模拟了定向凝固温度梯度方向与晶体择优生长方向间夹角及抽拉速度对柱状晶形态的影响, 模拟结果显示了不同择优生长取向柱状晶的竞争生长过程以及柱状晶尖端的分叉机制. 进而, 对NH4 Cl-H2 O透明体系进行了定向凝固实验, 模拟结果与实验结果吻合得很好. Yin等[25 ] 用Lattice Boltzmann方法求解温度场、浓度场和流场, 应用CA模型计算固液两相的转变, 研究了界面能各向异性和Gibbs-Thomson系数对枝晶尖端分叉机制的影响, 模拟结果显示, 当界面能各向异性和Gibbs-Thomson系数很小时, 枝晶尖端偏离择优生长方向, 出现高度分枝的现象. 此外, Zaeem等[55 ,56 ] 还将CA模型与PF模型进行了详细的对比分析, 说明了它们在模拟枝晶形态、计算效率及模型适用的模拟尺度等方面的优缺点及特性. ...
1
2000
... 早期的CA模型基本上都是针对二元合金系发展起来的, 实际应用的金属材料多为三元或多元合金. 近年来, 研究者们的关注焦点逐渐转向多元合金凝固过程的CA模型. 以往用CA模型模拟二元合金凝固组织形成时, 通常假设液相线斜率和平衡溶质分配系数为常数, 这与实际情况相差较大, 所以要准确计算固液界面溶质成分和溶质再分配过程, 必须耦合合金热力学计算. 2000年, Jarvis等[57 ] 用CAFE模型与商业软件Thermo-Calc相结合, 模拟了Al-Cu-Mg合金凝固过程的偏析, 并对比分析了对1D, 2D和3D凝固组织的模拟结果. 2007年, Zhu等[58 ] 借助于热力学软件PanEngine计算了多元合金的平衡液相线温度和平衡固相浓度, 在进行CA模拟时, 通过查表插值得到所需数据, 实现了动力学与热力学的弱耦合模拟. ...
1
2007
... 早期的CA模型基本上都是针对二元合金系发展起来的, 实际应用的金属材料多为三元或多元合金. 近年来, 研究者们的关注焦点逐渐转向多元合金凝固过程的CA模型. 以往用CA模型模拟二元合金凝固组织形成时, 通常假设液相线斜率和平衡溶质分配系数为常数, 这与实际情况相差较大, 所以要准确计算固液界面溶质成分和溶质再分配过程, 必须耦合合金热力学计算. 2000年, Jarvis等[57 ] 用CAFE模型与商业软件Thermo-Calc相结合, 模拟了Al-Cu-Mg合金凝固过程的偏析, 并对比分析了对1D, 2D和3D凝固组织的模拟结果. 2007年, Zhu等[58 ] 借助于热力学软件PanEngine计算了多元合金的平衡液相线温度和平衡固相浓度, 在进行CA模拟时, 通过查表插值得到所需数据, 实现了动力学与热力学的弱耦合模拟. ...
7
2012
... 实际上, 要真正反映凝固过程中合金成分变化的轨迹, 真实地再现多元合金凝固过程, 必须直接耦合计算合金热力学与凝固动力学. 此外, 在已往的模拟中, 人们通常假设溶质扩散系数为常数或者只依赖于温度, 忽略了合金成分的影响. 这对二元合金凝固过程模拟可以接受, 但对多元合金来说, 误差较大. 据此, 张显飞[59 ] 在考虑组元间相互作用的基础上建立了多元合金树枝晶生长的三维元胞自动机模型(3D CA), 并研发了直接耦合合金热力学与凝固动力学计算的模拟方法. 应用该模型模拟了Al-Cu-Mg合金定向凝固组织形成过程, 清晰地展示了枝晶生长过程, 如图8所示, 模拟预测与实验结果吻合得很好, 如图9所示. 模拟结果表明, 溶质扩散系数与合金成分有关, 合金元素间相互作用显著影响合金凝固过程, 如图10所示. ...
... Microstructural evolution in directionally solidified Al-11.6%Cu-0.85%Mg alloy (The temperature gradient in front of the S/L interface is 10 K/mm)[59 ] ...
... Al-11.6%Cu-0.85%Mg合金定向凝固组织演变过程[59 ] ...
... Dendrite spacing l for directionally solidified Al-11.6Cu-0.85Mg alloys[59 ] ...
... 定向凝固Al-11.6Cu-0.85Mg合金枝晶间距[59 ] ...
... Dendrite tip velocities calculated using different diffusion coefficients (Line 1 is the results calculated using the diffusion coefficients considering solute interactions, line 2 is the results calculated using the diffusion coefficients neglecting solute interactions)[59 ] ...
... 应用不同溶质扩散系数处理方法时计算的枝晶尖端生长速度随时间的变化[59 ] ...
7
2012
... 实际上, 要真正反映凝固过程中合金成分变化的轨迹, 真实地再现多元合金凝固过程, 必须直接耦合计算合金热力学与凝固动力学. 此外, 在已往的模拟中, 人们通常假设溶质扩散系数为常数或者只依赖于温度, 忽略了合金成分的影响. 这对二元合金凝固过程模拟可以接受, 但对多元合金来说, 误差较大. 据此, 张显飞[59 ] 在考虑组元间相互作用的基础上建立了多元合金树枝晶生长的三维元胞自动机模型(3D CA), 并研发了直接耦合合金热力学与凝固动力学计算的模拟方法. 应用该模型模拟了Al-Cu-Mg合金定向凝固组织形成过程, 清晰地展示了枝晶生长过程, 如图8所示, 模拟预测与实验结果吻合得很好, 如图9所示. 模拟结果表明, 溶质扩散系数与合金成分有关, 合金元素间相互作用显著影响合金凝固过程, 如图10所示. ...
... Microstructural evolution in directionally solidified Al-11.6%Cu-0.85%Mg alloy (The temperature gradient in front of the S/L interface is 10 K/mm)[59 ] ...
... Al-11.6%Cu-0.85%Mg合金定向凝固组织演变过程[59 ] ...
... Dendrite spacing l for directionally solidified Al-11.6Cu-0.85Mg alloys[59 ] ...
... 定向凝固Al-11.6Cu-0.85Mg合金枝晶间距[59 ] ...
... Dendrite tip velocities calculated using different diffusion coefficients (Line 1 is the results calculated using the diffusion coefficients considering solute interactions, line 2 is the results calculated using the diffusion coefficients neglecting solute interactions)[59 ] ...
... 应用不同溶质扩散系数处理方法时计算的枝晶尖端生长速度随时间的变化[59 ] ...
 (1)
(1)
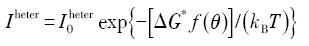 (2)
(2)
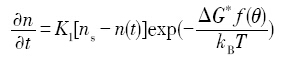 (3)
(3)
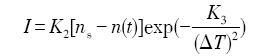 (4)
(4)
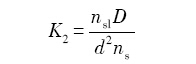 (5)
(5)
 (6)
(6)
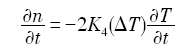 (7)
(7)
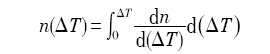 (8)
(8)
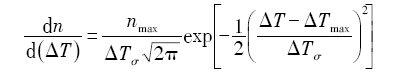 (9)
(9)
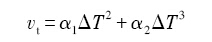 (10)
(10)
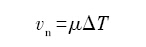 (11)
(11)
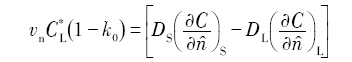 (12)
(12)
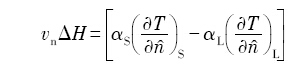 (13)
(13)
 (14)
(14)
 (15)
(15)
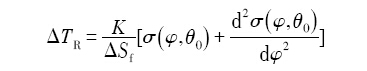 (16)
(16)
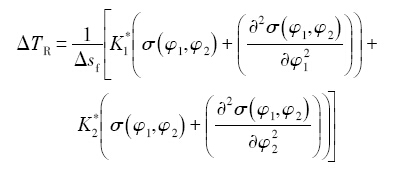 (17)
(17)
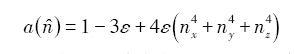 (18)
(18)
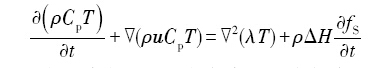 (19)
(19)
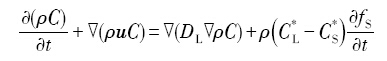 (20)
(20)
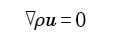 (21)
(21)
 (22)
(22)
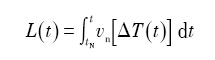 (23)
(23)
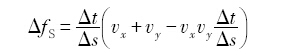 (24)
(24)
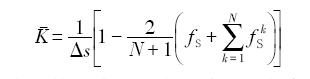 (25)
(25)
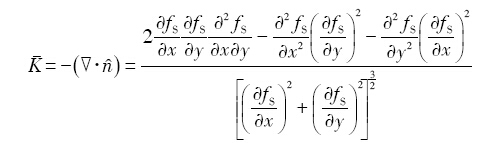 (26)
(26)
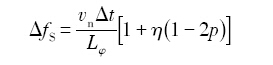 (27)
(27)
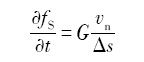 (28)
(28)
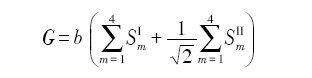 (29)
(29)
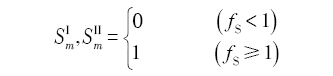 (30)
(30)
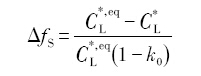 (31)
(31)
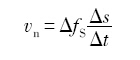 (32)
(32)
